2017-04-15

JavaScript

25 分钟读完 (大约 3772 个字)

parseInt() 与 parseFloat()

在 JavaScript 中，parseInt() 和 parseFloat() 的函数功能都是将所谓的数字字符串转化为一个真正的数值，但是两者在使用之上还是存在一定的区别的，它们两者之间的区别如下

parseFloat(string)，parseFloat() 函数可解析一个字符串，并返回一个浮点数，指定字符串中的首个字符是否是数字，如果是，则对字符串进行解析，直到到达数字的末端为止，然后以数字返回该数字，而不是作为字符串
parseInt(string, radix)，parseInt() 函数可解析一个字符串，并返回一个整数，radix 为进制，如果省略该参数或其值为 0，则数字将以 10 为基础来解析

差异

parseInt 和 parseFloat 都是将字符串类型转换为 number 类型，两者区别在于 parseFloat 会将 . 号转换为浮点数，而 parseInt 直接忽略停止转换

比如当处理 '5.12asc' 时，parseInt 直接转换为 5，parseFloat 则会转换为 5.12，parseInt 还可以指定第二位参数来指定转换结果的进制（2, 8, 16）（范围为 2 - 36）

parseFloat 与 NAN

parseFloat 会将它的字符串参数解析成为浮点数并返回，如果在解析过程中遇到了正负号（+ 或 -）、数字（0 - 9）、小数点，或者科学记数法中的指数（e 或 E）以外的字符，则它会忽略该字符以及之后的所有字符，返回当前已经解析到的浮点数

同时参数字符串首位的空白符会被忽略，如果参数字符串的第一个字符不能被解析成为数字，则 parseFloat 返回 NaN，根据 #parseFloat 可知，当调用 parseFloat 函数，是先转成字符串，再转为数字，如果不能转为数字，则返回 NaN，大体意思就是

如果返回的是基本类型，则将此返回值转为字符串，再尝试将字符串转为数字，如果不能转成数字则返回 NaN
如果 toString 方法返回的不是基本类型，则继续调用 valueOf 方法，如果返回的是基本类型，则将其转为字符串，再将字符串转为数字返回
如果 valueOf 方法返回的也不是基本类型，则返回 NaN

map(parseInt)

一个经典的问题

1 2	// 下面的语句返回什么 ['1', '2', '3'].map(parseInt)

你可能觉的会是 [1, 2, 3]，但实际的结果是 [1, NaN, NaN]，通常使用 parseInt 时，只需要传递一个参数，但实际上 parseInt 可以有两个参数，第二个参数是进制数，可以通过语句 'alert(parseInt.length) === 2' 来验证

map 方法在调用 callback 函数时，会给它传递三个参数，当前正在遍历的元素，元素索引，原数组本身，第三个参数 parseInt 会忽视，但第二个参数不会，也就是说 parseInt 把传过来的索引值当成进制数来使用，从而返回了 NaN，只需要稍微调整一下，正确的传递进制索引即可

1 2	// 返回 [1, 2, 3] ['1', '2', '3'].map(item => parseInt(item, 10))

parseFloat() 精度的问题

只有字符串中的第一个数字会被返回，开头和结尾的空格是允许的，需要注意的是，如果字符串的第一个字符不能被转换为数字，那么 parseFloat() 会返回 NaN，如果只想解析数字的整数部分，请使用 parseInt() 方法

parseFloat('10')         // 10

parseFloat('10.00')      // 10

parseFloat('10.33')      // 10.33

parseFloat('34 45 66')   // 34

parseFloat(' 60 ')       // 60

parseFloat('40 years')   // 40

parseFloat('He was 40')  // NaN

通过以上一些实例，我们对 parseFloat 的基本用法大致应该了解一些了，下面我们来看一些平常可能会遇到的问题，如下

var num = parseFloat('233333.9') - parseFloat('0.2')

// 233333.69999999998
console.log(num)

很明显结果并不是我们想要的样子，那么为什么会造成这种情况呢？其实最主要的原因就在于能被计算机读懂的是二进制，而不是十进制，我们来把 0.2 转换为二进制看一看

1	0.2 ==> 0.0011 0011 0011 0011 …

这样一看问题就很明显了，因为它是一个无限循环的小数，所以我们在平常过程当中需要做的就是尽量避免这样的情况发生，如果无法避免的话，可以采用以下几种方式来进行处理

// 第一种，四舍五入
Math.round(parseFloat('233333.9') - parseFloat(0.2))

// 第二种，保留几位小数
num.toFixed(2)  // toFixed(n) 中的 n 代表保留几位 

// 第三种，扩大一定的倍数，对结果在缩小这个倍数
var num1 = parseFloat('233333.9') * 1000000000000
var num2 = parseFloat('0.2') * 1000000000000
var num3 = (num1 - num2) / 1000000000000

另外还可以使用一些第三方库来进行解决，比如 bignumber

如何判断 0.1 + 0.2 与 0.3 相等

下面我们再来深入的探讨一下这个经典的面试题，也就是上面我们所提到的精度丢失的问题，说起原因，大家能回答出这是浮点数精度问题导致，也能辩证的看待这并非是 ECMAScript 这门语言的问题，今天我们就来具体看一下背后的原因

数字类型

ECMAScript 中的 Number 类型使用 IEEE754 标准来表示整数和浮点数值，所谓 IEEE754 标准，全称 IEEE 二进制浮点数算术标准，这个标准定义了表示浮点数的格式等内容，在 IEEE754 中，规定了四种表示浮点数值的方式

单精确度（32 位）
双精确度（64 位）
延伸单精确度
与延伸双精确度

像 ECMAScript 采用的就是双精确度，也就是说，会用 64 位字节来储存一个浮点数

浮点数转二进制

在展开这个问题之前，我们需要先了解计算机内部是如何表示数的，在计算机当中使用位来处理数据，每一个二进制数（二进制串）都一一对应一个十进制数，我们先来看下 1020 用十进制的表示，它是下面这样的

1	1020 = 1 * 10^3 + 0 * 10^2 + 2 * 10^1 + 0 * 10^0

而 1020 用二进制表示则是下面这样的

1	1020 = 1 * 2^9 + 1 * 2^8 + 1 * 2^7 + 1 * 2^6 + 1 * 2^5 + 1 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 0 * 2^0

所以我们可以得到 1020 的二进制为 1111111100，那如果是 0.75 用二进制表示呢？同理应该是

1	0.75 = a * 2^-1 + b * 2^-2 + c * 2^-3 + d * 2^-4 …

因为使用的是二进制，所以这里的 abcd … 的值的要么是 0 要么是 1，那怎么算出 abcd … 的值呢，我们可以两边不停的乘以 2 算出来，解法如下

1	0.75 = a * 2^-1 + b * 2^-2 + c * 2^-3 + d * 2^-4 …

两边同时乘以 2

1	1 + 0.5 = a * 2^0 + b * 2^-1 + c * 2^-2 + d * 2^-3 …

所以 a = 1，而剩下的

1	0.5 = b * 2^-1 + c * 2^-2 + d * 2^-3 …

再同时乘以 2

1	1 + 0 = b * 2^0 + c * 2^-2 + d * 2^-3 …

所以 b = 1，也就是说 0.75 用二进制表示就是 0.ab，也就是 0.11，然而不是所有的数都像 0.75 这么好算，我们来算下 0.1

0.1 = a * 2^-1 + b * 2^-2 + c * 2^-3 + d * 2^-4 … 

0 + 0.2 = a * 2^0 + b * 2^-1 + c * 2^-2 … （a = 0）
0 + 0.4 = b * 2^0 + c * 2^-1 + d * 2^-2 … （b = 0）
0 + 0.8 = c * 2^0 + d * 2^-1 + e * 2^-2 … （c = 0）
1 + 0.6 = d * 2^0 + e * 2^-1 + f * 2^-2 … （d = 1）
1 + 0.2 = e * 2^0 + f * 2^-1 + g * 2^-2 … （e = 1）
0 + 0.4 = f * 2^0 + g * 2^-1 + h * 2^-2 … （f = 0）
0 + 0.8 = g * 2^0 + h * 2^-1 + i * 2^-2 … （g = 0）
1 + 0.6 = h * 2^0 + i * 2^-1 + j * 2^-2 … （h = 1）

……

我们可以发现，这个计算在不停的循环，所以 0.1 用二进制表示就是 0.00011001100110011 …，而这是一个无限循环的二进制小数，这一点我们使用上面的 parseFloat() 也可以得知

1 2	// 0.0001100110011001100110011001100110011001100110011001101 parseFloat(0.1).toString(2)

但是我们可以发现，这里的结果为什么又不是一个无限循环的数了呢？而这个就要说起浮点数的存储

浮点数的存储

虽然 0.1 转成二进制时是一个无限循环的数，但计算机总要储存吧，我们知道 ECMAScript 使用 64 位字节来储存一个浮点数，那具体是怎么储存的呢？这就要说回 IEEE754 这个标准了，毕竟是这个标准规定了存储的方式，这个标准认为，一个浮点数（Value）可以这样表示

1	Value = sign * exponent * fraction

看起来很抽象的样子，其实简单理解的话就是科学计数法，比如 -1020，用科学计数法表示就是

1	-1 * 10^3 * 1.02

对应到上面的话，sign 就是 -1，exponent 就是 10^3，fraction 就是 1.02，而对于二进制也是一样，以 0.1 的二进制 0.00011001100110011 … 这个数来说可以表示为

1	1 * 2^-4 * 1.1001100110011 …

其中 sign 就是 1，exponent 就是 2^ - 4，fraction 就是 1.1001100110011 …，而当只做二进制科学计数法的表示时，这个 Value 的表示可以再具体一点变成

1	V = (-1)^S * (1 + Fraction) * 2^E

这里你可能会想，如果所有的浮点数都可以这样表示，那么我们存储的时候就把这其中会变化的一些值存储起来就好了，我们来一点点看，在上面的例子中，其中的 (-1)^S 表示符号位，当 S = 0，V 为正数，当 S = 1 时，V 为负数

再看 (1 + Fraction)，这是因为所有的浮点数都可以表示为 1.xxxx * 2^xxx 的形式，前面的一定是 1.xxx，那干脆我们就不存储这个 1 了，直接存后面的 xxxxx 好了，这也就是 Fraction 的部分，最后我们再来看看 2^E

如果是 1020.75，对应二进制数就是 1111111100.11，对应二进制科学计数法就是 1 * 1.11111110011 * 2^9，E 的值就是 9，而如果是 0.1，对应二进制是 1 * 1.1001100110011 … * 2^-4，E 的值就是 -4，也就是说 E 既可能是负数，又可能是正数，那问题就来了，那我们该怎么储存这个 E 呢？

我们这样解决，假如我们用 8 位字节来存储 E 这个数，如果只有正数的话，储存的值的范围是 0 ~ 254，而如果要储存正负数的话，值的范围就是 -127 ~ 127，我们在存储的时候，把要存储的数字加上 127，这样当我们存 -127 的时候，我们存 0，当存 127 的时候，存 254，这样就解决了存负数的问题，对应的当取值的时候，我们再减去 127

所以呢，真到实际存储的时候，我们并不会直接存储 E，而是会存储 E + bias，当用 8 个字节的时候，这个 bias 就是 127

所以，如果要存储一个浮点数，我们存 S，Fraction 和 E + bias 这三个值就好了，那具体要分配多少个字节位来存储这些数呢？IEEE754 给出了标准

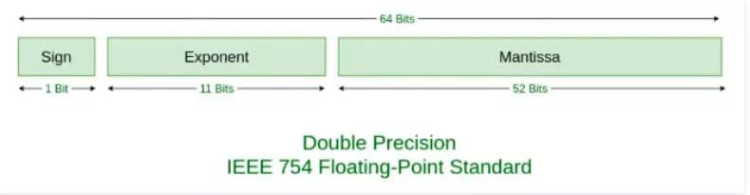
在这个标准下

我们会用 1 位存储 S，0 表示正数，1 表示负数
用 11 位存储 E + bias，对于 11 位来说，bias 的值是 2^(11-1) - 1，也就是 1023
用 52 位存储 Fraction

举个例子，就拿 0.1 来看，对应二进制是 1 * 1.1001100110011 … * 2^-4，Sign 是 0，E + bias 是 -4 + 1023 = 1019，1019 用二进制表示是 1111111011，Fraction 是 1001100110011 …

对应 64 个字节位的完整表示就是

1	0 01111111011 1001100110011001100110011001100110011001100110011010

同理，0.2 表示的完整表示是

1	0 01111111100 1001100110011001100110011001100110011001100110011010

所以当 0.1 存下来的时候，就已经发生了精度丢失，当我们用浮点数进行运算的时候，使用的其实是精度丢失后的数

浮点数的运算

关于浮点数的运算，一般由以下五个步骤完成

对阶
尾数运算
规格化
舍入处理
溢出判断

我们来简单看一下 0.1 和 0.2 的计算

首先是对阶，所谓对阶，就是把阶码调整为相同，比如 0.1 是 1.1001100110011 … * 2^-4，阶码是 -4，而 0.2 就是 1.10011001100110 … * 2^-3，阶码是 -3，两个阶码不同，所以先调整为相同的阶码再进行计算，调整原则是小阶对大阶，也就是 0.1 的 -4 调整为 -3，对应变成 0.11001100110011 … * 2^-3

接下来是尾数计算

  0.1100110011001100110011001100110011001100110011001101
+ 1.1001100110011001100110011001100110011001100110011010
————————————————————————————————————————————————————————
 10.0110011001100110011001100110011001100110011001100111

我们得到结果为 10.0110011001100110011001100110011001100110011001100111 * 2^-3，将这个结果处理一下，即结果规格化，变成 1.0011001100110011001100110011001100110011001100110011(1) * 2^-2

括号里的 1 意思是说计算后这个 1 超出了范围，所以要被舍弃了，再然后是舍入，四舍五入对应到二进制中，就是 0 舍 1 入，因为我们要把括号里的 1 丢了，所以这里会进一，结果就变成了

1	1.0011001100110011001100110011001100110011001100110100 * 2^-2

本来还有一个溢出判断，但是在这里我们就不过多涉及了，所以最终的结果存成 64 位就是

1	0 01111111101 0011001100110011001100110011001100110011001100110100

将它转换为 10 进制数就得到 0.30000000000000004440892098500626，因为两次存储时的精度丢失加上一次运算时的精度丢失，最终导致了 0.1 + 0.2 !== 0.3

解决方法

其实通过上面的介绍我们可以发现，二进制能精确地表示位数有限且分母是 2 的倍数的小数，比如 0.5，0.5 在计算机内部就没有舍入误差，所以 0.5 + 0.5 === 1

而在现实中，不同行业，要求的精度不是线性的，我们允许（对结果无关紧要的）误差存在，虽然允许误差存在，但是『永远不要直接比较两个浮点的大小』

一般在进行计算的时候，尽量将浮点运算转换成整数计算，整数是完全精度的，不存在舍入误差，如果非要计算一些浮点数，可以采用第三方库，比如之前提到过的 bignumber 等库来计算，使得在一定精度内，让浮点数计算结果符合我们的期望

{
  let x = new BigNumber(0.1)
  let y = new BigNumber(0.2)
  let z = new BigNumber(0.3)

  console.log(z.equals(x.add(y)))             // 0.3 === 0.1 + 0.2, true
  console.log(z.minus(x).equals(y))           // true
  console.log(z.minus(y).equals(x))           // true
}

{
  let x = 0.2
  console.log(x * x === 0.04)                 // false
  let y = new BigNumber(0.2)
  let r = y.mul(y)                            // 0.04
  console.log(r.equals(new BigNumber(0.04)))  // true
}

总结

为什么 0.1 + 0.2 不等于 0.3，因为计算机不能精确表示 0.1， 0.2 这样的浮点数，计算时使用的是带有舍入误差的数
并不是所有的浮点数在计算机内部都存在舍入误差，比如 0.5 就没有舍入误差
具有舍入误差的运算结可能会符合我们的期望，原因可能是负负得正，相互抵消这样的效果
怎么办？一是使用整型代替浮点数计算，二是不要直接比较两个浮点数，而应该使用 bignumber 这样的浮点数运算库

# JavaScript