线性表（单链表）

在之前的章节当中我们介绍了 线性表（顺序存储结构），它最大的缺点就是插入和删除的时候需要移动大量元素，这显然就需要耗费时间，如果我们想要解决这个问题，就需要考虑一下是如何导致这个问题出现的原因，即为什么当插入和删除的时候，需要移动大量元素？

其实简单来说，原因就是在于相邻两元素的存储位置也具有邻居关系，它们在内存中的位置是紧挨着的，所以无法快速的插入和删除，如果想要解决这个问题，就可以使用今天我们将要介绍的『链式存储结构』

链式存储结构

线性表的链式存储结构的特点就是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以存在内存中未被占用的任意位置，比起顺序存储结构每个数据元素只需要存储一个位置就可以了，而在链式存储结构中，除了要存储元素信息外，还要存储它的后继元素的存储地址（指针），也就是说出了存储其本身的信息外，还需要存储一个指示其直接后继的存储位置的信息

我们把存粗数据元素信息的域称为『数据域』，把存储直接后继位置的域称为『指针域』，指针域中存储的信息称为『指针域链』，这两部分信息组成数据元素称为存储映像，也称之为『结点』（Node），这里有一个需要注意的地方，就是注意区分『节点』和『结点』，具体区别如下

• 节点通常被认为是一个实体，有处理能力，比如网络上的一台计算机
• 而结点则只是一个交叉点，打个结，做个标记，仅此而已
• 要记住，一般算法中点的都是『结点』

我们在数据结构的图形表示中，对于数据集合中的每一个数据元素用中间标有元素值的方框表示，一般称它为数据结点，简称结点，而在链表数据结构中，链表中每一个元素称为『结点』，每个结点都应包括两个部分

• 一个是需要用的实际数据 data
• 另一个就是存储下一个结点地址的指针，即数据域和指针域

数据结构中的每一个数据结点对应于一个存储单元，这种储存单元称为储存结点，也可简称结点

单链表

比如 n 个结点链接成一个链表，即为线性表（a1，a2，a3 … an）的链式存储结构，因为此链表的每个结点中只包含一个指针域，所以叫做单链表，如下图所示

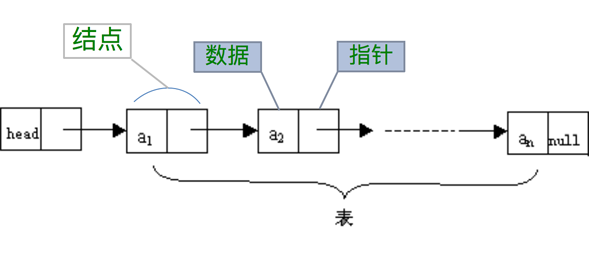
对于线性表来说，存在头部和尾部，链表也不例外，我们把链表中的第一个结点的存储位置称为『头指针』，最后一个结点称为『空』（null）

头指针域头结点

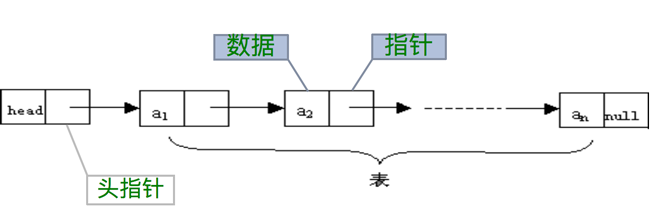
通过之前的内容我们可以知道，头结点的数据域一般是不存储任何信息的，那么又与头指针有什么区别呢

• 头指针
  • 是指链表指向第一个结点的指针，如果链表有头结点，则是指向头结点的指针
  • 头指针具有标识作用，所以常用头指针冠以链表的名字（指针变量的名字）
  • 无论链表是否为空，头指针『均不为空』
  • 头指针是链表的『必要元素』
• 头结点
  • 头结点是为了操作的统一和方便而设立的，放在第一个元素的结点之前，其数据域一般无意义（但也可以用来存放链表的长度）
  • 有了头结点，对在第一元素结点前插入和删除的操作就可以与其他结点的操作相统一
  • 头结点不一定是链表的必须要素（非必要元素）

单链表的示例如下

空链表的示例如下

单链表存储结构

我们在 C 语言中可以使用结构指针来描述单链表

1
2
3
4
5
6

typedef struct Node {
  ElemType data;      // 数据域
  struct Node* Next;  // 指针域
} Node;

typedef struct Node* LinkList;

再次强调，我们一般看到的结点是由『存放数据元素的数据域』和『存放后继结点地址的指针域』组成，比如我们假设 p 是指向线性表第 i 个元素的指针，则该结点 ai 的『数据域』我们可以用 p -> data 的值来进行表示（它是一个数据元素），而结点 ai 的指针域可以用 p -> next 来进行表示（它的值是一个指针），所以我们可以推断出 p -> next 是指向第 i + 1 个元素的，也就是指向 ai + 1 的指针

同理，如果 p -> data = ai，那么 p -> next -> data = ai + 1 的，而在 JavaScript 当中，我们设计链表包含两个类，一个是 Node 类用来表示结点，另一个是 LinkedList 类提供插入结点、删除结点等一些操作，Node 类包含两个属性

• element 用来保结点点上的数据
• next 用来保存指向下一个结点的链接

具体实现如下

1
2
3
4
5

// 结点
function Node(element) {
  this.element = element   // 当前结点的元素
  this.next = null         // 下一个结点链接
}

而 LinkedList 类提供了对链表进行操作的方法，包括插入删除结点，查找给定的值等，值得注意的是，它只有一个属性，那就是使用一个 Node 对象来保存该链表的头结点，实现如下

1
2
3
4
5
6
7
8
9

// 链表类
function LList() {
  this.head = new Node('head')  // 头结点
  this.find = find              // 查找结点
  this.insert = insert          // 插入结点
  this.remove = remove          // 删除结点
  this.findPrev = findPrev      // 查找前一个结点
  this.display = display        // 显示链表
}

单链表的读取

在线性表的顺序存储结构中，我们要计算任意一个元素的存储位置是很容易的，直接获取元素的下标即可，但是在单链表中，由于第 i 个元素的位置我们是不知道的，所以必须要从第一个结点开始挨个查找，代码如下

1
2
3
4
5
6
7
8

// 查找结点
function find(item) {
  var currNode = this.head
  while (currNode.element !== item) {
    currNode = currNode.next
  }
  return currNode
}

find 方法同时展示了如何在链表上移动，首先创建一个新结点，将链表的头结点赋给这个新创建的结点，然后在链表上循环，如果当前结点的 element 属性和我们要找的信息不符，就将当前结点移动到下一个结点，如果查找成功，该方法返回包含该数据的结点，否则就会返回 null

单链表的插入

我们先来看下单链表但插入，假设存储元素 e 但结点为 s，要实现结点 p，p -> next 和结点 s 之间逻辑关系但变化，可以参考下图

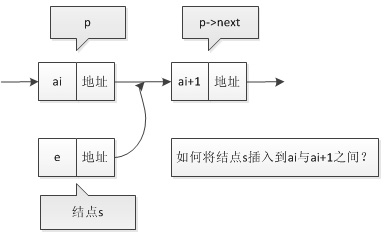
其实简单来说，并没有那么复杂，我们只需要按照如下简单操作即可

• 先 s -> next = p -> next
• 再 p -> next = s

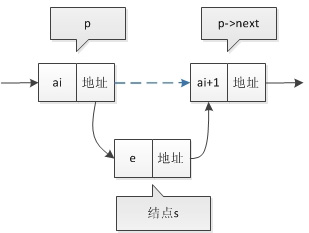
但是这里有个需要注意的地方，即上面两者的操作顺序是不可颠倒的，即

• 先 p -> next = s
• 再 s -> next = p -> next

但是这样一来，如果先执行 p -> next 的话会先被覆盖为 s 的地址，那么在执行 s -> next = p -> next 就相当于执行 s -> next = s 了，可以发现，这是一个死循环，所以这两者的顺序一定不要弄反了

在上面我们实现了 find() 方法，有了 find() 方法以后，我们就可以十分简便的来实现插入操作了，只需要将新结点的 next 属性设置为后面结点的 next 属性对应的值，然后设置后面结点的 next 属性指向新的结点

1
2
3
4
5
6
7

// 插入结点
function insert(newElement, item) {
  var newNode = new Node(newElement)
  var currNode = this.find(item)
  newNode.next = currNode.next
  currNode.next = newNode
}

单链表的删除

流程可以如下所示

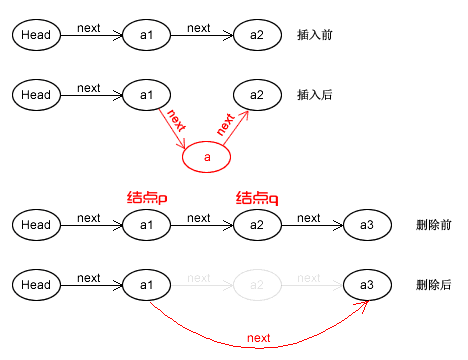
假设元素 a2 的结点为 q，要实现结点 q 删除单链表的操作，其实就是将它的前继结点的指针绕过，指向后继结点即可，所以我们所要做的操作实际上就是一步

• 可以 p -> next = p -> next -> next
• 也可以先让 q = p -> next 然后 p -> next = q -> next

从链表中删除结点时，我们先要找到待删除结点的前一个结点，找到后，我们修改它的 next 属性，使其不在指向待删除的结点，而是待删除结点的下一个结点

那么，我们就得需要定义一个 findPrev 方法遍历链表，检查每一个结点的下一个结点是否存储待删除的数据，如果找到，返回该结点，这样就可以修改它的 next 属性了

1
2
3
4
5
6
7
8

// 查找前一个结点
function findPrev(item) {
  var currNode = this.head
  while (currNode.next !== null && currNode.next.element !== item) {
    currNode = currNode.next
  }
  return currNode
}

这样一来，remove 方法的实现也就迎刃而解了

1
2
3
4
5
6
7
8
9

// 删除结点
function remove(item) {
  var prevNode = this.findPrev(item)
  var currNode = this.find(item)
  if (prevNode.next !== null) {
    prevNode.next = prevNode.next.next
    currNode.next = null
  }
}

效率对比

通过上面的操作我们可以发现，无论是单链表插入还是删除算法，它们其实都是由两个部分组成

• 第一部分就是遍历查找第 i 个元素
• 第二部分就是实现插入和删除操作

从整个算法来说，我们很容易可以推出它们的时间复杂度都是 O(n)，如果在我们不知道第 i 个元素的指针位置，单链表数据结构在插入和删除操作上与线性表的顺序存储结构是没有太大优势的，但是如果我们希望从第 i 个位置开始，插入连续 10 个元素

• 对于顺序存储结构意味着，每一次插入都需要移动 n - i 个位置，所以每次都是 O(n)
• 而对于单链表，我们只需要在第一次时，找到第 i 个位置的指针，此时为 O(n)，但是接下来只是简单地通过赋值移动指针而已，时间复杂度都是 O(1)

显然，对于插入或删除数据越频繁的操作，单链表的效率优势就越是明显

测试

最后我们将代码综合起来，在测试一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

/**
 * 一个简单的单向链表
 * @param element 
 */

// 结点
function Node(element) {
  this.element = element        // 当前结点的元素
  this.next = null              // 下一个结点链接
}

// 链表类
function LList() {
  this.head = new Node('head')  // 头结点
  this.find = find              // 查找结点
  this.insert = insert          // 插入结点
  this.remove = remove          // 删除结点
  this.findPrev = findPrev      // 查找前一个结点
  this.display = display        // 显示链表
}

// 查找结点
function find(item) {
  var currNode = this.head
  while (currNode.element !== item) {
    currNode = currNode.next
  }
  return currNode
}

// 插入结点
function insert(newElement, item) {
  var newNode = new Node(newElement)
  var currNode = this.find(item)
  newNode.next = currNode.next
  currNode.next = newNode
}

// 删除结点
function remove(item) {
  var prevNode = this.findPrev(item)
  var currNode = this.find(item)
  if (prevNode.next !== null) {
    prevNode.next = prevNode.next.next
    currNode.next = null
  }
}

// 查找前一个结点
function findPrev(item) {
  var currNode = this.head
  while (currNode.next !== null && currNode.next.element !== item) {
    currNode = currNode.next
  }
  return currNode
}

// 显示链表
function display() {
  var currNode = this.head
  while (currNode.next !== null) {
    currNode = currNode.next
    console.log(currNode.element)
  }
}

var llist = new LList()

llist.insert('111', 'head')
llist.insert('222', '111')
llist.insert('333', '222')
llist.insert('444', '333')

llist.display()
llist.remove('222')

llist.display()

单链表整表创建

对于顺序存储结构的线性表的『整表创建』，我们可以用数组的初始化来直观理解，而单链表和顺序存储结构就不一样了，它不像顺序存储结构数据这么集中，它的数据可以是分散在内存各个角落的，它的增长也是动态的，对于每个链表来说，它所占用空间的大小和位置是不需要预先分配划定的，可以根据系统的情况和实际的需求即时生成

创建单链表的过程是一个动态生成链表的过程，从『空表』的初始状态起，依次建立各元素结点并逐个插入链表，所以单链表整表创建的算法思路如下

• 声明一个结点 p 和计数器变量 i
• 初始化一空链表 L
• 让 L 的头结点的指针指向 null，即建立一个带头结点的单链表
• 循环实现后继结点的赋值和插入

而创建的方式通常又有两种，即『头插法』和『尾插法』，下面我就一个一个来看

头插法

头插法从一个空表开始，生成新结点，读取数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上，直到结束为止，简单来说就是把新加进的元素放在表头后的第一个位置，然后

• 先让新节点的 next 指向头节点之后
• 然后让表头的 next 指向新节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

/* 头插法建立单链表示例 */
void CreateListHead(LinkList *L, int n) {
  LinkList p;
  int i;

  // 初始化随机数种子
  srand(time(0));

  *L = (LinkList)malloc(sizeof(Node));
  (*L) -> next = NULL;

  for(i = 0; i < n; i++) {
    // 生成新结点
    p = (LinkList)malloc(sizeof(Node));
    p -> data = rand() % 100 + 1;
    p -> next = (*L) -> next;
    (*L) -> next = p;
  }
}

尾插法

头插法建立链表虽然算法简单，但是生成的链表中结点的次序和输入的顺序相反（即是从右向左的），所以在某些场景下就不太适合，所以我们可以采用把新结点都插入到最后，也就是所谓的尾插法（正常方向，从右向左）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

/* 尾插法建立单链表演示 */
void CreateListTail(LinkList *L, int n) {
  LinkList p, r;
  int i;

  srand(time(0));
  *L = (LinkList)malloc(sizeof(Node));

  // 多了这一步，r 是指向尾部的结点
  r = *L;

  for(i = 0; i < n; i++) {
    p = (Node *)malloc(sizeof(Node));
    p -> data = rand() % 100 + 1;
    r -> next = p;

    // 这一句需要说明一下
    // 即我们每次新建一个新的结点 p，然后把 p 赋值给 r
    // 这时新的结点就成了 r，然后再次创建一个结点 p，依次循环
    r = p;
  }

  r -> next = NULL;
}

单链表整表删除

当我们不打算使用这个单链表当时候，我们需要把它销毁，其实也就是在内存中将它释放掉，以便留出空间给其他程序或软件来进行使用，单链表整表删除的思路如下

• 声明结点 p 和 q
• 将第一个结点赋值给 p，下一个结点赋值给 q
• 循环执行释放 p，然后将 q 赋值给 p

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Status ClearList(LinkList *L) {

  LinkList p, q;
  p = (*L) -> next;

  while (p) {
    q = p -> next;
    free(p);
    p = q;
  }

  (*L) -> next = NULL;
  return OK;
}

这里会存在一个问题，可不可以直接剔除掉 q，直接写成 free(p) 和 p = p -> next 呢，答案是不可以的，原因是我们知道，p 是一个结点，它除了有数据域，还有指针域，当我们进行 free(p) 的时候，其实是对它整个结点进行删除和内存释放的工作，而我们的整表删除是需要一个一个结点来进行删除的，所以我们就需要使用一个临时变量 q 来记载 p 的下一个结点

单链表结构与顺序存储结构优缺点

我们分别从存储分配方式、时间性能、空间性能三方面来进行对比

存储分配方式

• 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素
• 单链表采用链式存储结构，用一组任意的存储单元存放线性表的元素

时间性能

• 查找
  • 顺序存储结构 O(1)
  • 单链表 O(n)
• 插入和删除
  • 顺序存储结构需要平均移动表长一半的元素，时间复杂度为 O(n)
  • 单链表在计算出某位置的指针后（这时的复杂度为 O(n)），但是插入和删除时间仅为 O(1)

空间性能

• 顺序存储结构需要预分配存储空间，分大了，容易造成空间浪费，分小了，容易发生溢出
• 单链表不需要分配存储空间，只要有就可以分配，元素个数也不受限制

综上所述对比，我们得出一些比较实用的结论

• 若线性表需要频繁查找，很少进行插入和删除操作时，可以采用顺序存储结构
• 若需要频繁插入和删除时，可以采用单链表结构
• 当线性表中的元素个数变化较大或者根本不知道有多大时，最好用单链表结构，这样可以不需要考虑存储空间的大小问题
• 而如果事先知道线性表的大致长度，比如一年十二个月，一周就是星期一至星期日共七天，这种用顺序存储结构效率会高很多

总之，线性表的顺序存储结构和单链表结构各有其优缺点，不能简单的说哪个好，哪个不好，需要根据实际情况，来综合平衡采用哪种数据结构更能满足和达到需求和性能

如何快速找到未知长度单链表的中间结点

最后的最后，我们再来看一个网上比较流行的单链表面试题，关于这个题目的解法有两种，我们一个一个来看，比较常规的解法就是，首先遍历一遍单链表用来确定单链表的长度 L，然后再次从头结点出发循环 L/2 次来找到单链表的中间结点，由此可知，其算法的复杂度为 O(L + L/2) = O(3L/2)，这里我们之所以没有简化，是为来与后面的方法来进行对比

我们主要来看一下下面这个很巧妙的方法，即利用『快慢指针』的方法，主要原理如下（这也是标尺的思想）

• 设置两个指针 *search、*mid 都指向单链表的头节点
• 其中 *search 的移动速度是 *mid 的 2 倍
• 当 *search 指向末尾节点的时候，*mid 正好就在中间了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Status GetMidNode(LinkList L, ElemType *e) {

  LinkList search, mid;
  mid = search = L;

  while (search -> next != NULL) {
    // search 的移动速度是 mid 的两倍
    if (search -> next -> next != NULL) {
      search = search -> next -> next;
      mid = mid -> next;
    } else {
      search = search -> next;
    }
  }
  
  *e = mid -> data; 
  return OK;
}