我们在之前的章节当中介绍过了 线性表(单链表) ,对于单链表而言,由于每个结点只存储了向后的指针,到了尾部标识就停止了向后链的操作(也就是 null,空指针),所以说按照这样的方式,只能索引后继结点而不能索引前驱结点,所引起的问题也是显而易见的,比如如果不从头结点出发,就无法访问到全部结点,遇到这种情况,我们就可以采用我们今天将要介绍到的循环链表
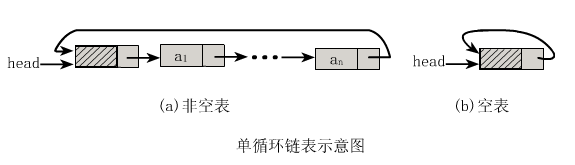
循环链表 要解决单链表里面遇到的问题其实也并不麻烦,我们只需要将单链表中的终端结点的指针(null)由空指针改为指向头结点就可以解决,这样一来整个单链表就形成了一个环,这种头尾相接的单链表也就成为了单循环链表,简称为『循环链表』,如下图所示
但是这里需要注意,并不是说循环链表一定要有头结点,其实循环链表和单链表的主要差异就在于循环的判断空链表的条件上
单链表只需要判断 head -> next 是否为 null 即可
但是单链表则需要判断 head -> next 是否等于 head
下面我们就来看看单循环链表的代码如何实现,其实本质上和我们在 线性表(单链表) 一节当中实现的单链表差异不大,只是在单链表的基础上,将尾节点的指针指向头结点,就构成了一个循环链表,环形链表从任意一个节点开始,都可以遍历整个链表
1 this .head.next = this .head
在下面的约瑟夫问题当中我们可以看到具体的应用
约瑟夫问题 下面我们来看一个比较近经典的问题,约瑟夫问题,问题是这样的
据说在罗马人占领乔塔帕特后,39 个犹太人与约瑟夫及他的朋友躲到一个洞中,39 个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41 个人排成一个圆圈,由第 1 个人开始报数,每报数到第 3 人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止,然而约瑟夫和他的朋友并不想遵从,约瑟夫要他的朋友先假装遵从,他将朋友与自己安排在第 16 个与第 31 个位置,于是逃过了这场死亡游戏
看到这个问题我们首先想到的是要用到循环链表,还有就是要计算链表中有多少个元素,这两点很重要,再有就是找到当前节点和在链表中向前移动 m 个节点,其实简单来说就是在初始化链表的时候我们定义一个当前节点,将它赋值为头节点 this.currentNode = this.head,这样在移动节点的时候就可以用它指向下一个节点,向前移动节点的时候有个地方需要注意,如果当前移动到头节点上需要再向前移动一个节点 this.currentNode.next.next
下面我们来看如何实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 function Node (element ) this .element = element this .next = null } function LList ( this .head = new Node('head' ) this .find = find this .insert = insert this .remove = remove this .findPrev = findPrev this .display = display this .head.next = this .head this .currentNode = this .head this .advance = advance this .count = count } function find (item ) var currNode = this .head while (currNode.element != item) { currNode = currNode.next } return currNode } function insert (newElement, item ) var newNode = new Node(newElement) var current = this .find(item) newNode.next = current.next current.next = newNode } function findPrev (item ) var currNode = this .head while (!(currNode.next == null ) && (currNode.next.element != item)) { currNode = currNode.next } return currNode } function remove (item ) var prevNode = this .findPrev(item) if (prevNode.next !== null ) { prevNode.next = prevNode.next.next } } function advance (n ) while (n > 0 ) { if (this .currentNode.next.element == 'head' ) { this .currentNode = this .currentNode.next.next } else { this .currentNode = this .currentNode.next } n-- } } function count ( var node = this .head var i = 0 while (!(node.next.element == 'head' )) { node = node.next i++ } return i } function display ( var currNode = this .head while (!(currNode.next == null ) && !(currNode.next.element == 'head' )) { document .write(currNode.next.element + ' ' ) currNode = currNode.next } } var llist = new LList()llist.insert('1' , 'head' ) llist.insert('2' , '1' ) llist.insert('3' , '2' ) llist.insert('4' , '3' ) llist.insert('5' , '4' ) llist.insert('6' , '5' ) llist.insert('7' , '6' ) llist.insert('8' , '7' ) llist.insert('9' , '8' ) llist.insert('10' , '9' ) llist.display() document .write('<br>' )var n = 3 while (llist.count() > 2 ) { llist.advance(n) llist.remove(llist.currentNode.element) llist.display() document .write('<br>' ) }
最终结果如下
我们假设只有十个人,所以一个站在队伍的第四位,一个站在队伍的第十位,到最后会只剩下他们两个人
循环链表的特点 在单链表中,我们有了头结点时,我们可以用 O(1) 的时间访问第一个结点,但对于要访问最后一个结点,我们必须要挨个向下索引,所以需要 O(n) 的时间,如果使用循环链表的话,用 O(1) 的时间就可以由链表指针访问到最后一个结点,可以参考开头部分的单循环链表示意图,但是在此之前,我们先来稍微的调整一下,不再和开头的时候一样,而是采用指向终端结点的尾指针来表示循环链表,此时查找开始结点和终端结点都很方便了
如下图
但是相对应的,我们的判断条件也需要相对的调整一下,即判断是否为空链表的条件应该调整为判断 rear 是否等于 rear -> next,循环链表的特点是无须增加存储量,仅对链接方式稍作改变,即可使得表处理更加方便灵活
判断链表中是否有环 我们来看一个在平常当中经常会遇到的关于循环链表的问题,那就是如何判断链表中是否有环,有环的定义是,链表的尾节点指向了链表中的某个节点,如下图所示
我们可以发现在第六个位置的指针是指向第三个位置的,那么我们如何判断这种情况呢?下面我们就来尝试一下,链表的生成还是使用我们之前的代码,不过是简化过的,只保留几个最基本的方法方便我们测试就行,如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 function Node (element ) this .element = element this .next = null } function LList ( this .head = new Node('head' ) this .find = find this .insert = insert this .getHead = getHead this .head.next = this .head this .flag = 0 } function find (item ) var currNode = this .head while (currNode.element != item) { currNode = currNode.next } return currNode } function insert (newElement, item ) var newNode = new Node(newElement) var current = this .find(item) newNode.next = current.next current.next = newNode } function getHead ( return this .head } var llist = new LList()llist.insert('1' , 'head' ) llist.insert('2' , '1' ) llist.insert('3' , '2' ) llist.insert('4' , '3' ) llist.insert('5' , '4' ) llist.find('5' ).next = llist.find('2' ) var list = llist.getHead()
有了链表以后,我们就可以来看看如何判断链表中是否有环,主要有三种方式,我们一个一个来看
哈希表 第一种方法,创建哈希表,不过会占用较大的空间,不是最佳方法(时间复杂度 O(n)),它的原理是遍历链表,将链表各节点添加至哈希表中,添加前判断此节点是否已存在哈希表中,存在的话说明链表中存在环
1 2 3 4 5 6 7 8 9 10 11 12 13 function test (list ) var set = new Set() while (list) { if (set .has(list)) { console .log(`存在环` ) console .log(list) return true } set .add(list) list = list.next } return set }
测试结果如下
检测到节点 2 是重复项,说明存在环
访问标记 另外一种方式就是给节点添加 flag 访问标记,时间复杂度 O(n),不过这种方法不需要额外的空间
1 2 3 4 5 6 7 8 9 10 11 function test (list ) while (list) { if (list.flag) { console .log(`存在环` ) console .log(list) return true } list.flag = 1 list = list.next } }
遍历链表,每访问一个新节点,使其 flag 为 1,每次访问节点前先判断其 flag 是否为 1,为 1 则是已访问过的节点,说明链表中存在环,测试结果如下
1 2 3 test(list) console .log(list)
快慢指针 这个也是业界流传最广的方法,设定快指针 fast,慢指针 slow,每次循环快指针 fast 移动两个位置,慢指针移动一个位置(时间复杂度 O(n),需要额外的空间),如果在某个时候 fast === slow,表示存在环
1 2 3 4 5 6 7 8 9 10 11 function test (list ) var fast = list.next.next, slow = list.next while (list) { if (fast === slow) { console .log(`存在环` ) return true } fast = fast.next.next slow = slow.next } }
测试结果如下