2020-02-22

Essay

16 分钟读完 (大约 2356 个字)

栈和队列

从本章开始，我们来看两个平常可能听到的比较多的名词，那就是栈和队列，其实严格意义上来说，栈和队列也属于线性表，因为它们也都用于存储逻辑关系为『一对一』的数据，但由于它们比较特殊，所以我们在此将它们两个单独拿出来进行了解

使用栈结构存储数据，讲究『先进后出』，即最先进栈的数据，最后出栈，而使用队列存储数据，讲究『先进先出』，即最先进队列的数据，也最先出队列，既然栈和队列都属于线性表，所以根据线性表分为顺序表和链表的特点，栈也可分为顺序栈和链表，队列也分为顺序队列和链队列

因为篇幅有限，本篇主要介绍栈的相关内容，而关于队列的相关内容可以见队列

栈的定义

栈是一种重要的线性结构，也是线性表的一种具体形式，我们来列举一些生活当中比较常见的例子，比如浏览器的前进后退键，某些编辑工具的撤销功能等等，都是利用栈的基本原理实现的，它的官方定义如下

栈（Stack）是一个后进先出（Last in first out，LIFO）的线性表，它要求只在表尾进行删除和插入操作

其实简单来说，所谓的栈，其实也就是一个特殊的线性表（顺序表、链表），但是它在操作上有一些特殊的要求和限制

栈的元素必须『后进先出』
栈的操作只能在这个线性表的表尾进行
对于栈来说，这个表尾称为栈的栈顶（top），相应的表头称为栈底（bottom）
再次强调，表尾是栈顶，表头是栈底

栈的插入和删除操作

栈的插入操作（push），叫做进栈，也称为压栈，入栈，类似子弹放入弹夹的动作
栈的删除操作（pop），叫做出栈，也称为弹栈，如同弹夹中的子弹出夹

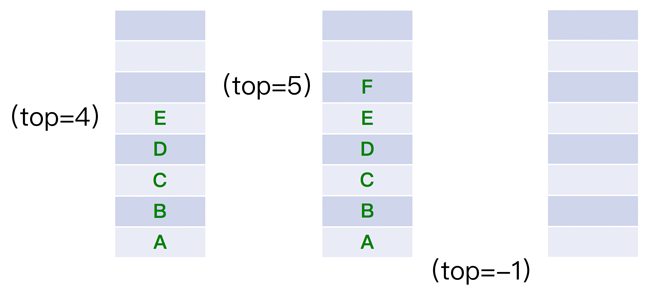
因为栈的本质是一个『线性表』，线性表有两种存储形式，那么栈也有分为『栈的顺序存储结构』和『栈的链式存储结构』，最开始栈中不含有任何数据，叫做『空栈』，此时栈顶就是栈底，然后数据从栈顶进入，栈顶栈底分离，整个栈的当前容量变大，数据出栈时从栈顶弹出，栈顶下移，整个栈的当前容量变小

如下图所示

创建一个栈

首先先来定义存储结构

typedef int ElemType;

typedef struct {
  ElemType *base;
  ElemType *top;
  int stackSize;
} sqStack;

我们在这里定义了一个顺序存储的栈，它包含了三个元素 base，top，stackSize

base 是指向栈底的指针变量
top 是指向栈顶的指针变量
stackSize 指示栈的当前可使用的最大容量

但是这里可以发现，我们与之前定义的方式不太一样，比如没有 data 元素存放数据，又或者为什么会有两个 ElemType 元素？其实上面定义方式对应下图

其实我们也可以像下面这样来进行声明

typedef int ElemType;

typedef struct {
  ElemType data[MAXSIZE];
  
  // 用于标注栈顶的位置
  int top;
  int stackSize;
}

对应下图

栈的初始化操作如下

#define STACK_INIT_SIZE 100

initStack(sqStack *s) {
  s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
  if (!s->base)
    exit(0);

  // 最开始，栈顶就是栈底
  s->top = s->base;
  s->stackSize = STACK_INIT_SIZE;
}

入栈操作和出栈操作

入栈操作又叫『压栈操作』，就是向栈中存放数据，入栈操作要在『栈顶』进行，每次向栈中压入一个数据，top 指针就要 + 1，直到栈满为止

#define SATCKINCREMENT 10

Push(sqStack *s, ElemType e) {
  // 如果栈满，追加空间
  if (s->top – s->base >= s->stackSize) {
    s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
    if (!s->base)
      exit(0);

    s->top = s->base + s->stackSize;              // 设置栈顶
    s->stackSize = s->stackSize + STACKINCREMENT; // 设置栈的最大容量
  }

  *(s->top) = e;
  s->top++;
}

相对应的，出栈操作就是在栈顶取出数据，栈顶指针随之下移的操作，每当从栈内弹出一个数据，栈的当前容量就 - 1，代码如下

Pop(sqStack *s, ElemType *e) {
  if (s->top == s->base)  // 重合表示栈已经为空
    return;
  *e = *--(s->top);       // 先减减，在赋值
}

清空一个栈

所谓清空一个栈，就是将栈中的元素全部作废，但栈本身物理空间并不发生改变（注意不是销毁），因此我们只要将 s -> top 的内容赋值为 s -> base 即可，这样 s -> base 等于 s -> top，也就表明这个栈是空的了（类似于高级格式化只是但单纯地清空文件列表而没有覆盖硬盘的原理是一样的）

代码如下

1
2
3

ClearStack(sqStack *s){
  s->top = s->base;
}

销毁一个栈

销毁一个栈与清空一个栈不同，销毁一个栈是要释放掉该栈所占据的物理内存空间，因此不要把销毁一个栈与清空一个栈这两种操作混淆

DestroyStack(sqStack *s) {
  int i, len;
  len = s->stackSize;
  for (i = 0; i < len; i++) {
    free(s->base);
    s->base++;
  }
  s->base = s->top = NULL;
  s->stackSize = 0;
}

计算栈的当前容量

计算栈的当前容量也就是计算栈中元素的个数，因此只要返回 s.top - s.base 即可，注意，栈的最大容量是指该栈占据内存空间的大小，其值是 s.stackSize，它与栈的当前容量不是一个概念

int StackLen(sqStack s) {
  // 这里需要注意，这里是两个地址相减，它的结果并不是两个地址的一个差值
  // 如果两个地址是指向整形的话，它们相减是表示它们之间相隔几个元素
  // 需要注意的是，两个地址的类型要相同，而且是不能相加的
  return(s.top – s.base);
}

栈的链式存储结构

栈的链式存储结构，简称『栈链』，通常我们用的都是栈的顺序存储结构存储，所以这里我们只是简单的了解一下栈链，栈因为只是栈顶来做插入和删除操作，所以比较好的方法就是将栈顶放在单链表的头部，栈顶指针和单链表的头指针合二为一，如下图所示

初始化如下

teypedef struct StackNode {
  ElemType data;      // 存放栈的数据
  struct StackNode *next;
} StackNode, *LinkStackPtr;

teypedef struct LinkStack {
  LinkStackPrt top;   // top 指针
  int count;          // 栈元素计数器
}

进栈操作

对于栈链的 Push 操作，假设元素值为 e 的新结点是 s，top 为栈顶指针

Status Push(LinkStack *s, ElemType e) {
  LinkStackPtr p = (LinkStackPtr)malloc(sizeof(StackNode));
  p->data = e;
  p->next = s->top;
  s->top = p;
  s->count++;
  return OK;
}

出栈操作

至于链栈的出战 Pop 操作，假设变量 p 用来存储要删除的栈顶结点，将栈顶指针下移一位，最后释放 p 即可

Status Pop(LinkStack *s, ElemType *e) {
  LinkStackPtr p;

  // 判断是否为空栈
  if (StackEmpty(*s))
    return ERROR;

  *e = s->top->data;
  p = s->top;
  s->top = s->top->next;

  free(p);
  
  s->count--;
  return OK;
}

JavaScript 中的栈的实现

最后的最后，我们再来看下在 JavaScript 当中如何实现栈的数据结构，同样的，它也有两种方式来进行实现，分别是『链式存储』和『顺序存储』，下面我们一个一个来进行了解

顺序存储

这个理解起来十分简单，因为在 JavaScript 当中，我们可以使用内置的数组对象轻松实现，而且语言本身也提供来我们许多方法，直接使用就可以了，代码如下

class Stack {
  constructor() {
    this.items = []
  }

  push(value) {
    this.items.push(value)
  }

  pop() {
    return this.items.pop()
  }

  top() {
    return this.items[this.items.length - 1]
  }

  isEmpty() {
    return this.items.length === 0
  }

  clear() {
    return this.items = []
  }

  size() {
    return this.items.length
  }

  display() {
    return this.items.toString()
  }
}

var stack = new Stack()

stack.push(5)
stack.push(6)
stack.push(7)

stack.display()
stack.pop()
stack.top()
stack.isEmpty()
stack.size()
stack.clear()
stack.size()
stack.display()

链式存储

链式存储这个一般使用较少，了解即可，代码如下

function Stack() {
  let Node = function (ele) {
    this.ele = ele
    this.next = null
  }

  let length = 0, top = null

  this.push = function (ele) {
    let node = new Node(ele)
    top ? node.next = top : top = node
    top = node
    length++
  }

  this.pop = function () {
    let current = top
    if (top) {
      top = current.next
      current.next = null
      length--
      return current
    } else {
      return 'null stack'
    }
  }

  this.top = function () {
    return top
  }

  this.size = function () {
    return length
  }

  this.display = function () {
    let text = ''
    current = top
    while (current) {
      text += current.ele + ' '
      current = current.next
    }
    return text
  }

  this.clear = function () {
    top = null
    length = 0
  }
}

var stack = new Stack()

stack.push(5)
stack.push(6)
stack.push(7)

stack.display()
stack.pop()
stack.pop()
stack.top()
stack.clear()
stack.display()

# Essay