在之前的章节当中我们介绍过了 栈 的相关知识,本篇我们就接着上篇未完的内容来了解一下和栈十分相似的队列的相关知识
什么是队列
简单来说,队列类似于『链表』,也是存储数据的结构,队列中数据进入队列的顺序很重要,一般来说,队列就是一群人或者事物按照排好的顺序等待接受服务或者处理,比如我们常见的排队买票就是一个典型的队列
队列的定义
队列(Queue)是只允许在一端进行插入操作,而在另一端进行删除操作的『线性表』,与栈相反,队列是一种先进先出(First In First Out,FIFO)的线性表,与栈相同的是,队列也是一种重要的线性结构,实现一个队列同样需要顺序表或链表作为基础,如下图所示

队列既可以用链表实现,也可以用顺序表实现,跟栈相反的是,栈一般我们用『顺序表』来实现,而队列我们常用『链表』来实现,简称为『链队列』,定义如下
1
2
3
4
5
6
7
8
9
| typedef struct QNode {
ElemType data;
struct QNode *next;
} QNode, *QueuePrt;
typedef struct {
QueuePrt front, rear;
} LinkQueue;
|
队列的链式存储结构
我们将队头指针指向链队列的头结点,而队尾指针指向终端结点,但是需要注意的是,头结点不是必要的(在这里我们为了方便操作,选择将其添加上)

当队列为空时,front 和 rear 都指向头结点

创建一个队列
创建一个队列要完成两个任务,一是在内存中创建一个头结点,二是将队列的头指针和尾指针都指向这个生成的头结点(因为此时是空队列)
1
2
3
4
5
6
7
8
| initQueue(LinkQueue *q) {
q->front = q->rear = (QueuePtr)malloc(sizeof(QNode));
if (!q->front)
exit(0);
q->front->next = NULL;
}
|
入队列操作
总的来说分为三个步骤,如下图所示



代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
| InsertQueue(LinkQueue *q, ElemType e) {
QueuePtr p;
p = (QueuePtr)malloc(sizeof(QNode));
if (p == NULL)
exit(0);
p->data = e;
p->next = NULL;
q->rear->next = p;
q->rear = p;
}
|
出队列操作
出队列操作是将队列中的第一个元素移出,队头指针不发生改变,改变头结点的 next 指针即可,如下所示


但是这里有一个需要注意的地方,就是如果原队列只有一个元素,那么我们就应该处理一下队尾指针


代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| DeleteQueue(LinkQueue *q, ELemType *e) {
QueuePtr p;
if (q->front == q->rear)
return;
p = q->front->next;
*e = p->data;
q->front->next = p->next;
if (q->rear == p)
q->rear = q->front;
free(p);
}
|
销毁一个队列
由于链队列建立在内存的动态区,因此当一个队列不再有用时应当把它及时销毁掉,以免过多地占用内存空间,方式很简单,如下
1
2
3
4
5
6
7
| DestroyQueue(LinkQueue *q) {
while (q->front) {
q->rear = q->front->next;
free(q->front);
q->front = q->rear;
}
}
|
队列的顺序存储结构
之前我们提到过,在队列的实现上我们更愿意用链式存储结构来存储,那么为什么会这样呢?
我们假设一个队列有 n 个元素,则顺序存储的队列需建立一个大于 n 的存储单元,并把队列的所有元素存储在数组的前 n 个单元,数组下标为 0 的一端则是队头,如下图所示

入队列操作其实就是在队尾追加一个元素,不需要任何移动,时间复杂度为 O(1),而出队列则不同,因为我们已经假设下标为 0 的位置是队列的队头,因此每次出队列操作所有元素都要向前移动,所以当前的时间复杂度为 O(n)
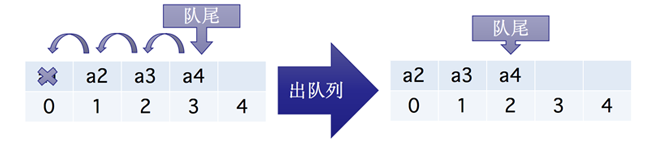
但是这里我们可以想到,如果我们不去限制队头一定要在下标为 0 的位置,那么出队列的操作就是不是不需要移动全体元素了呢?看下面这个图

但是这样也会出现一些问题,例如按下边的情形继续入队列,就会出现数组越界的错误

但是通过上图可以发现,我们还有 0 和 1 两个下标还空着在,这就是所谓的『假溢出』
循环队列定义
通过上面的例子,我们可以知道,要解决假溢出的办法就是如果后面满了,就再从头开始,也就是头尾相接的循环,也就是这里我们要说的『循环队列』,循环队列它的容量是固定的,并且它的队头和队尾指针都可以随着元素入出队列而发生改变,这样循环队列逻辑上就好像是一个环形存储空间,但要需要注意的是,在实际的内存当中,不可能有真正的环形存储区,我们只是用顺序表模拟出来的逻辑上的循环,可以通过下图来进行了解

通过上图我们可以发现,似乎循环队列的实现只需要灵活改变 front 和 rear 指针即可,也就是让 front 或 rear 指针不断加 1,即使超出了地址范围,也会自动从头开始,所以在这里我们可以采取取模运算(取余数)的方式来进行处理,因为它取到的值永远不会大于除数,如下
1
2
| (rear + 1) % QueueSize
(front + 1) % QueueSize
|
循环队列的相关操作
代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#define MAXSIZE 100
typedef struct {
ElemType *base;
int front;
int rear;
}
initQueue(cycleQueue *q) {
q->base = (ElemType *)malloc(MAXSIZE * sizeof(ElemType));
if (!q->base)
exit(0);
q->front = q->rear = 0;
}
InsertQueue(cycleQueue *q, ElemType e) {
if ((q->rear + 1) % MAXSIZE == q->front)
return;
q->base[q->rear] = e;
q->rear = (q->rear + 1) % MAXSIZE;
}
DeleteQueue(cycleQueue *q, ElemType *e) {
if (q->front == q->rear)
return;
*e = q->base[q->front];
q->front = (q->front + 1) % MAXSIZE;
}
|
JavaScript 中的队列实现
最后我们再来看下在 JavaScript 当中如何实现队列,这里需要注意了,栈一般我们用『顺序表』来实现,而队列一般是采用『链表』来实现的(链队列),同样的,它也有两种方式来进行实现,分别是『链式存储』和『顺序存储』,下面我们一个一个来进行了解
链式存储
代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| function Queue() {
let Node = function (ele) {
this.ele = ele
this.next = null
}
let length = 0, front = null, rear = null
this.push = function (ele) {
let node = new Node(ele), temp = null
if (length == 0) {
front = node
} else {
temp = rear
temp.next = node
}
rear = node
length++
}
this.pop = function () {
let temp = front
front = front.next
length--
temp.next = null
return temp
}
this.size = function () {
return length
}
this.getFront = function () {
return front
}
this.getRear = function () {
return rear
}
this.display = function () {
let text = '', temp = front
while (temp) {
text += temp.ele + ' '
temp = temp.next
}
return text
}
this.clear = function () {
front = null
rear = null
length = 0
}
}
let queue = new Queue()
queue.push(1)
queue.push(2)
queue.push(3)
queue.push(4)
queue.display()
queue.pop()
queue.push(5)
queue.display()
|
顺序存储
同栈一样,在 JavaScript 当中,我们可以使用内置的数组对象轻松实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| function Queue() {
var arr = []
this.push = function (element) {
arr.push(element)
}
this.pop = function () {
return arr.shift()
}
this.getFront = function () {
return arr[0]
}
this.getRear = function () {
return arr[arr.length - 1]
}
this.clear = function () {
arr = []
}
this.size = function () {
return length
}
this.diplay = function() {
return arr.toString()
}
}
let queue = new Queue()
queue.push(1)
queue.push(2)
queue.push(3)
queue.push(4)
queue.display()
queue.pop()
queue.push(5)
queue.display()
|




















