递归
2020-03-05
Essay
31 分钟 读完 (大约 4724 个字)

递归

递归（Recursion algorithm）在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法，递归式方法可以被用于解决很多的计算机科学问题，因此它是计算机科学中十分重要的一个概念，绝大多数编程语言支持函数的自调用，在这些语言中函数可以通过调用自身来进行递归，在平常可以说是经常可以听到的概念，今天我们就来深入的了解一下，什么是递归，以及递归的一些相关应用

什么是递归

简单来说，在编程语言中，函数直接或间接调用函数本身，则该函数称为『递归函数』，我们可以用数学代入法来理解，假设我们用递归来算阶乘 f(n)，常用的方式是这样的

1
2
3
4
5
6
function factorial(n) {
  return n === 1 ? 1 : n * factorial(n - 1)
}

// 也可以使用箭头函数来进行简化
const factorial = (x) => (x == 0 ? 1 : x * factorial(x - 1))

我们可以发现，在 f 的里面再次用到了 f，我们把它展开了来看看

1
2
3
4
5
6
7
8
9
10
11
12
f(6)
=> 6 * f(5)
=> 6 * (5 * f(4))
=> 6 * (5 * (4 * f(3)))
=> 6 * (5 * (4 * (3 * f(2))))
=> 6 * (5 * (4 * (3 * (2 * f(1)))))
=> 6 * (5 * (4 * (3 * (2 * 1))))
=> 6 * (5 * (4 * (3 * 2)))
=> 6 * (5 * (4 * 6))
=> 6 * (5 * 24)
=> 6 * 120
=> 720

也就是下图这样

通过上面的拆解，我们可以发现，其实就是先递进，再回归，而这就是『递归』，比如下面这个多级对象遍历的示例，就是递归的实际应用，也是我们平常开发当中经常会遇到的问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
var treeNodes = [{
  id: 1,
  name: '1',
  children: [{
    id: 11,
    name: '11',
    children: [{
      id: 111,
      name: '111',
      children: []
    }, {
      id: 112,
      name: '112'
    }]
  }, {
    id: 12,
    name: '12',
    children: []
  }],
  users: []
}]

function parseTreeJson(treeNodes) {
  if (!treeNodes || !treeNodes.length) return
  for (var i = 0, len = treeNodes.length; i < len; i++) {
    var childs = treeNodes[i].children
    console.log(treeNodes[i].id)
    if (childs && childs.length > 0) {
      parseTreeJson(childs)
    }
  }
}

parseTreeJson(treeNodes)

斐波那契数列

我们下面来看一个实际的应用场景，也算是递归的经典应用场景，那就是斐波那契数列，我们先来看看不使用递归如何来实现斐波那契（Fibonacci）数列，如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <stdio.h>

int main() {
  int i;
  int a[40];

  a[0] = 0;
  a[1] = 1;
  printf("%d %d ", a[0], a[1]);

  for (i = 2; i < 40; i++) {
    a[i] = a[i - 1] + a[i - 2];
    printf("%d ", a[i]);
  }

  return 0;
}

在上面代码中，我们使用循环从 i = 2 开始进行迭代，然后输出每一步对应的值，不过看上去就很麻烦的样子，下面我们在用递归的方式改写一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>

int Fib(int i) {
  if (i < 2) {
    return i == 0 ? 0 : 1;
  }

  return Fib(i - 1) + Fib(i - 2);
}

int main() {
  int i;
  for (i = 0; i < 40; i++) {
    printf("%d ", Fib(i));
  }

  return 0;
}

这样可以发现代码就很清晰了，拆解后如下图所示

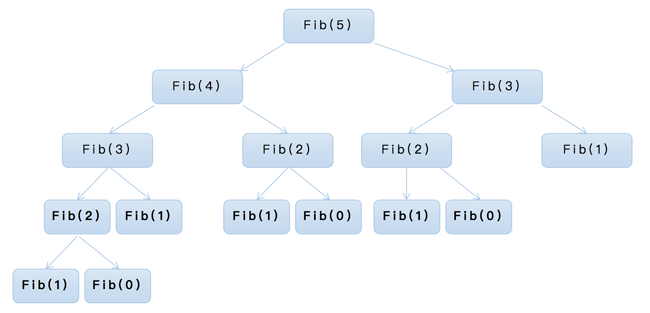
JavaScript 当中的实现方式如下

1
2
3
4
5
6
7
function fibonacci(n) {
  return n <= 1 ? 1 : fibonacci(n - 1) + fibonacci(n - 2)
}

for (let i = 0; i <= 10; i++) {
  console.log(fibonacci(i))
}

上面是最为基本的实现方式，但是我们可以利用记忆函数来对其进行优化，也就是将之前运算过的结果保存下来，对于频繁依赖之前结果的计算能够节省大量的时间，但是也存在一定的缺点，那就是闭包中的 obj 对象会额外占用内存，如下

1
2
3
4
5
6
7
8
9
const memory = function (fn) {
  let obj = {}
  return function (n) {
    if (obj[n] === undefined) obj[n] = fn(n)
    return obj[n]
  }
}

fibonacci = memory(fibonacci)

另外使用『动态规划』会比之前实现的空间复杂度更低，也是更推荐的解法

1
2
3
4
5
6
7
8
9
10
11
12
13
function fibonacci_DP(n) {
  let res = 1
  if (n === 1 && n === 2) return res
  n = n - 2
  let cur = 1, pre = 1
  while (n) {
    res = cur + pre
    pre = cur
    cur = res
    n--
  }
  return res
}

尾调用

在上面我们介绍了斐波那契数列的实现，在这里我们多提一点，那就是 尾调用 的使用，它的作用是利用在某个函数的最后一步是调用另一个函数的方式来进行优化，我们需要做的就是把所有用到的内部变量改写成函数的参数，比如我们使用尾调用来优化我们上面提到的斐波那契数列和阶乘

阶乘优化

1
2
3
4
5
function factorial(n, total) {
  return n === 1 ? total : factorial(n - 1, n * total)
}

factorial(5, 1)  // 120

斐波纳契数列优化

1
2
3
4
5
6
7
function fibonacci(n, n1 = 1, n2 = 1) {
  return n <= 1 ? n2 : fibonacci(n - 1, n2, n1 + n2)
}

for (let i = 0; i <= 10; i++) {
  console.log(fibonacci(i))
}

递归定义

之前我们通过了斐波那契数列的示例简单的了解了一下什么是递归，下面我们就来看看递归的具体含义

在高级语言中，函数自己调用和调用其他函数并没有本质的不同，我们把一个直接调用自己或通过一系列的调用语句间接地调用自己的函数，称作『递归函数』，不过，递归程序最怕的就是陷入永不结束的无穷递归中，所以需要注意，每个递归定义必须至少有一个条件，当满足这个条件时递归不再进行，即函数不再调用自身而是返回值，比如之前我们的 Fbi 函数结束条件就是 i < 2

之前我们对比了两种实现斐波那契的代码，迭代和递归的区别是

  • 迭代使用的是循环结构
  • 递归使用的是选择结构

使用递归能使程序的结构更清晰、更简洁、更容易让人理解，从而减少读懂代码的时间，但大量的递归调用会建立函数的副本，会消耗大量的时间和内存，而迭代则不需要此种付出，所以需要根据当前环境进行考虑使用，递归函数分为调用和回退阶段，递归的回退顺序是它调用顺序的逆序

分治思想

分而治之的思想古已有之，秦灭六国，统一天下正是采取各个击破、分而治之的原则，而分治思想在算法设计中也是非常常见的，当一个问题规模较大且不易求解的时候，就可以考虑将问题分成几个小的模块，逐一解决，因为采用分治思想处理问题，其各个小模块通常具有与大问题相同的结构，这种特性也使递归技术有了用武之地，下面我们就通过一个实例来了解一下

汉诺塔

汉诺塔问题，它是用递归方法求解的一个典型问题，题目是这样的

塔上有三根柱子和一套直径各不相同的空心圆盘，开始时源柱子上的所有圆盘都按从大到小的顺序排列，目标是通过每一次移动一个圆盘到另一根柱子上，最终把一堆圆盘移动到目标柱子上，过程中不允许把较大的圆盘放置在较小的圆盘上

如下图所示

把一堆圆盘从一个柱子移动另一根柱子，必要时需要使用辅助的柱子，这样一来我们可以把它分为三个子问题

  • 首先，移动一对圆盘中较小的圆盘到辅助柱子上，从而露出下面较大的圆盘
  • 其次，移动下面的圆盘到目标柱子上
  • 最后，将刚才较小的圆盘从辅助柱子上在移动到目标柱子上

再把三个步骤转化为简单数学问题

  • 把 n - 1 个盘子由 A 移到 B
  • 把第 n 个盘子由 A 移到 C
  • 把 n - 1 个盘子由 B 移到 C

这样问题解决了，但实际操作中，只有第二步可直接完成，而第一、三步又成为移动的新问题，以上操作的实质是把移动 n 个盘子的问题转化为移动 n - 1 个盘，那一、三步如何解决？

事实上上述方法设盘子数为 n，n 可为任意数，该法同样适用于移动 n - 1 个盘，因此依据上法，可解决 n - 1 个盘子从 A 杆移到 B 杆（第一步）或从 B 杆移到 C 杆（第三步）问题，所以现在的问题就是由移动 n 个盘子的操作转化为移动 n - 2 个盘子的操作，依据该原理层层递推，即可将原问题转化为解决移动 n - 2，n - 3 … 3、2，直到移动 1 个盘的操作，而移动一个盘的操作是可以直接完成的

至此，我们的任务算作是真正完成了，而这种由繁化简，用简单的问题和已知的操作运算来解决复杂问题的方法，就是递归法，我们先来看看如何使用 C 语言来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <stdio.h>

// 将 n 个盘子从 x 借助 y 移动到 z
void move(int n, char x, char y, char z) {
  if (1 == n) {
    printf("%c --> %c\n", x, z);
  } else {
    move(n - 1, x, z, y);         // 将 n-1 个盘子从 x 借助 z 移到 y 上
    printf("%c --> %c\n", x, z);  // 将 第 n 个盘子从 x 移到 z 上
    move(n - 1, y, x, z);         // 将 n-1 个盘子从 y 借助 x 移到 z 上
  }
}

int main() {
  int n;

  printf("请输入汉诺塔的层数: ");
  scanf("%d", &n);
  printf("移动的步骤如下: \n");
  move(n, 'X', 'Y', 'Z');

  return 0;
}

下面再来看看使用 JavaScript 如何实现，其实本质上原理是一致的

1
2
3
4
5
6
7
8
9
var hanoi = function (num, x, y, z) {
  if (num > 0) {
    hanoi(num - 1, x, z, y)
    console.log(' 移动 ' + num + ' 号圆盘' + ' 从 ' + x + ' 移动到 ' + z)
    hanoi(num - 1, y, x, z)
  }
}

hanoi(3, 'A', 'B', 'C')

运行结果如下

1
2
3
4
5
6
7
移动 1 号圆盘 从 A 移动到 C
移动 2 号圆盘 从 A 移动到 B
移动 1 号圆盘 从 C 移动到 B
移动 3 号圆盘 从 A 移动到 C
移动 1 号圆盘 从 B 移动到 A
移动 2 号圆盘 从 B 移动到 C
移动 1 号圆盘 从 A 移动到 C

其实简单总结就是

  • 目标是 x ==> z
  • 第一步 x ==> y（借助 z）
  • 第二步 y ==> z（借助 x）

最终，我们的操作结果可以由下图所示

八皇后问题

最后我们再来看一下八皇后问题，八皇后问题是一个古老而著名的问题，是回溯算法的典型例题，问题是这样的，在 8 x 8 格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法？如下图，便是其中一种实现方式

那么到底什么是『回溯法』呢？我们慢慢来看，我们首先将棋盘调整的小一些，这样比较方便描述，结果如下

那么现在问题变成了 4 皇后问题了，现在我们把第一个皇后放在第一个格子，被涂黑的地方是不能放皇后的，便成为了下面这样的方式

这时我们可以发现，第二行的皇后只能放在第三格或第四格，比方我们放第三格

这时可以发现，前两位皇后已经把第三行全部锁死了，即第三位皇后无论放在第三行任何位置都会被吃掉，所以我们可以得出，在第一个皇后位于 1 号，第二个皇后位于 3 号的情况下问题无解，显然此时我们只能返回上一步，来给 2 号皇后换个位置，如下

这时可以发现，第三个皇后只有一个位置可选，但是当第三个皇后占据第三行蓝色空位时，第四行皇后无路可走，于是也会发生错误，所以这是我们就需要再次返回上层调整三号皇后的位置，但是三号皇后没有别的地方可以安排，所以继续返回到第二层来进行调整，但是二号皇后也是同样的情况，那么我们只能调整一号皇后的位置了，于是我们将一号皇后的位置稍微调整一下以便我们继续搜索，也就是下图这样的情况

说到这里，应该就已经对『回溯法』已经有了基本概念，下面我们就来看看如何使用代码来进行实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <math.h>
using namespace std;

int n = 8;
int total = 0;
int *c = new int(n);

bool is_ok(int row) {
  for (int j = 0; j != row; j++) {
    if (c[row] == c[j] || row - c[row] == j - c[j] || row + c[row] == j + c[j])
      return false;
  }
  return true;
}

void queen(int row) {
  if (row == n)
    total++;
  else
    for (int col = 0; col != n; col++) {
      c[row] = col;
      if (is_ok(row))
        queen(row + 1);
    }
}

int main() {
  queen(0);
  cout << total;
  return 1;
}

其实代码主要的逻辑就是下面的十行代码

1
2
3
4
5
6
7
8
9
10
void queen(int row) {
  if (row == n)
    total++;
  else
    for (int col = 0; col != n; col++) {
      c[row] = col;
      if (is_ok(row))
        queen(row + 1);
    }
}

算法是逐行安排皇后的，其参数 row 为现在正执行到第几行，n 表示的是皇后数，代码第二行比较好理解，如果程序当前能正常执行到第八行，那自然是找到了一种解法，于是八皇后问题解法数加 1

如果当前还没排到第八行，则进入 else 语句，遍历所有列 col，将当前 col 存储在数组 c 里，然后使用 is_ok() 检查 row 行 col 列能不能摆皇后，若能摆皇后，则递归调用 queen 去安排下一列摆皇后的问题，下面我们一步一步来逐步拆解了解

  1. 刚开始的时候 row = 0，意思是要对第 0 行摆皇后操作，if 判断失败，进入 else，进入 for 循环，col 初始化为 0，显然，0 行 0 列的位置一定可以摆皇后的，因为这是第一个皇后，于是 is_ok(0) 测试成功，递归调用 queen(1) 安排第一行的皇后
  2. 在第一行时 row = 1，进来 if 依然测试失败，进入 for 循环，col 初始化为 0，第 1 行第 0 列显然是不能摆皇后的，因为 0 行 0 列已经有了一个皇后，于是 is_ok() 测试失败，循环什么也不做空转一圈，col 变为 1，1 行 1 列依然 is_ok() 测试失败，一直到 1 行 2 列，发现可以摆皇后，于是继续递归 queen(2) 去安排第二个皇后位置
  3. 如果在某种情况下问题无解呢？例如前面在 4 皇后问题中，0 行 0 列摆皇后是无解的，假设前面递归到 queen(2) 时候，发现第 2 行没有地方可以摆皇后，那怎么办呢？但是这时要注意 queen(2) 的调用是在 queen(1) 的 for 循环框架内的，queen(2) 若无解，则自然而然 queen(1) 的 for 循环 col 自加 1，即将第 1 行的皇后从 1 行 2 列改为 1 行 3 列的位置，检查可否放皇后后继续安排下一行的皇后
  4. 如此递归，当 queen(0) 的 col 自加到 7，说明第一列的皇后已经遍历了从 0 行 1 列到 0 行 7 列，此时 for 循环结束，程序退出，所以此时我们就可以在主函数中调用 queen(0)，得到正确结果（八皇后问题一共有 92 种解法）

看完了 C 语言的版本，我们再来看看如何使用 JavaScript 来进行实现，首先尝试使用嵌套 for 循环实现，发现只能找出第一种解法，没办法统计到所有的解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
var n = 8
var arr = []
var total = 0

function b() {
  for (var row = 0; row <= n;) {
    if (row == n) {
      total++
      break
    } else {
      var col = 0

      if (arr[row] != undefined) {
        // 说明是回溯回来重新选择位置的，要从上次的位置开始往后选
        var col = arr[row] + 1
      }
      
      for (; col <= n; col++) {
        if (col == n) {
          // 当前行的所有列都走完了，都没有位置可以放棋子，则从上一行开始从新选择位置
          arr[row] = undefined
          row--
          if (row)
            break
        }

        if (isOk(row, col)) {
          arr[row] = col
          row++
          break
        }
      }
    }
  }
}

function isOk(row, col) {
  for (var i = 0; i < row; i++) {
    if (row == 0) {
      // 第一行随便放哪个位置都行
      return true
    }
    if (arr[i] == col || Math.abs(arr[i] - col) == Math.abs(i - row)) {
      // 同一行，同一列或者斜对角线都不能放
      return false
    }
  }
  // 成功比较完了之前的所有行，说明这个位置可以放置
  return true
}

b()
console.info(total)

可以发现，for 循环的实现太过复杂，当找到一个解法后，希望移动第一行的棋子，寻找其他解法时，这个时候，当回溯到第一行时，无法控制棋子的位置（比如已经从第 0 个位置移到 2 的位置才寻找到了第一种解法，当寻找其他解法时，回溯到第一行时，就不应该在返回 0 和 1 这个两个位置），而 for 循环是无法记录的

所以这里我们采用递归来进行实现，此时每一行的 for 循环都能被记住当前是第几列（也就是上面所说的 queen(2) 的调用是在 queen(1) 的 for 循环框架内的）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
var arr = []
var arr2 = []
var total = 0

function ab(row) {
  if (row == n) {
    // 当 row 已经成功走到最后一行，说明已经找到了一种解法，找到一种解法，就把当前的位置记录下来
    arr2.push([].slice.call(arr))
    total++
  }

  for (var col = 0; col < n; col++) {
    if (isOk(row, col)) {
      // 当前行的这一列不与前几行的位置冲突，则把这个位置记录下来，位置记录下来，是为了每次循环比较是否有冲突
      arr[row] = col
      // 进入下一行选位置，因为递归，所以当里层的循环全部结束以后，会返回上一层继续循环，实现了回溯
      ab(row + 1)
    }
  }
}

// 这个方法同上
function isOk(row, col) {
  for (var i = 0; i < row; i++) {
    if (row == 0) {
      return true
    }
    if (arr[i] == col || Math.abs(arr[i] - col) == Math.abs(i - row)) {
      return false
    }
  }
  return true
}

ab(0)
console.info(total)
console.info(arr2)
# Essay
BF 和 KMP 算法
队列

评论

分类

标签云

Angular CSS Essay GIS HTTP JavaScript Node.js React Vue

最新文章

归档

标签

Angular 15
CSS 14
Essay 29
GIS 11
HTTP 11
JavaScript 45
Node.js 14
React 20
Vue 5
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×