2020-03-22

Essay

19 分钟读完 (大约 2865 个字)

二叉树

在前一章当中，我们介绍了树的相关概念，但是普通的树，我们在平时使用是较少的，而一些比较特殊的树则是使用较多的，比如二叉树的使用范围就较为广泛，也最具有代表意义，因此在本章当中我们将会重点讨论二叉树

二叉树的定义

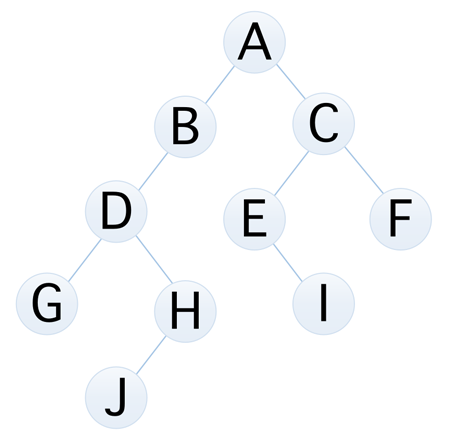
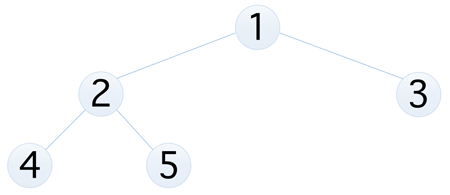
二叉树（Binary Tree）是 n（n >= 0）个结点的『有限集合』，该集合或者为空集（空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成，比如下面这个图，就一个普通的二叉树

二叉树的特点

二叉树的每个结点最多有两棵子树，所以二叉树中不存在度大于二的结点，但是需要注意的是，不是都需要两棵子树，而是最多可以是两棵，没有子树或者有一棵子树也都是可以的，而且左子树和右子树是有顺序的，次序不能颠倒，即使树中某结点只有一棵子树，也要区分它是左子树还是右子树，比如下图的两种情况就是两个完全不同的二叉树

二叉树的五种基本形态

分为以下五种形态

空二叉树
只有一个根结点
根结点只有左子树
根结点只有右子树
根结点既有左子树又有右子树

分别对应下图的五种情况，特别需要注意的是第一种空二叉树的情况

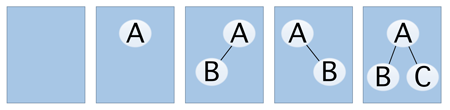
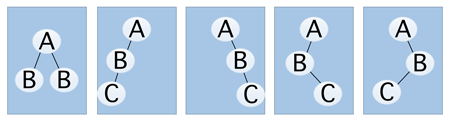
但是我们若只从形态上来考虑，拥有三个结点的普通树只有两种情况，即两层或者三层，但是对于二叉树来说，由于要区分左右，所以就演变成了下面五种形态

特殊二叉树

看完了上面五种形态的二叉树，我们再来看一些特殊的二叉树

斜树

顾名思义，斜树是一定要斜的，但斜也分为左右两种情况，比如下图当中的两种情况

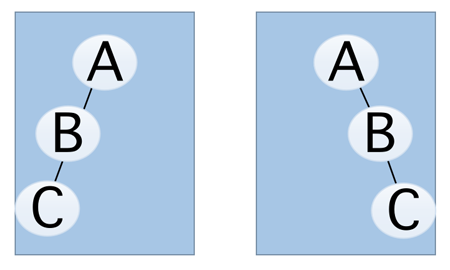
但是需要注意的是，方向必须是在同一方向上，如下图便不能称之为斜树

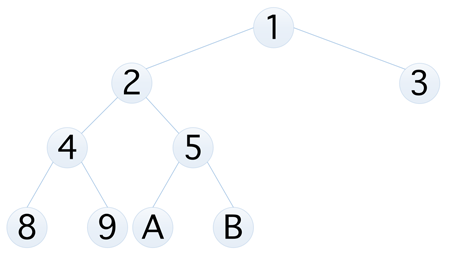
满二叉树

从字面上就能看出，满二叉树指的就是完美二叉树，也就是在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树，也就是下图这样的情况

满二叉树的特点有下面这些

叶子只能出现在最下一层
非叶子结点的度一定是二
在同样深度的二叉树中，满二叉树的结点个数一定最多，同时叶子也是最多

注意和下面的完全二叉树进行区分

完全二叉树

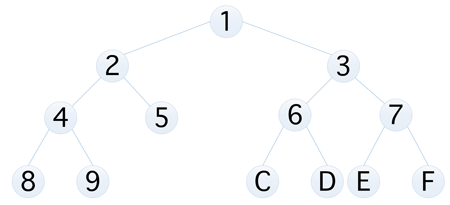
那么什么是完全二叉树呢？对于一棵具有 n 个结点的二叉树按层序编号，如果编号为 i（1 <= i <=n）的结点与同样深度的满二叉树中编号为 i 的结点位置完全相同，则这棵二叉树称为完全二叉树，比如下面两种情况都可以称之为完全二叉树

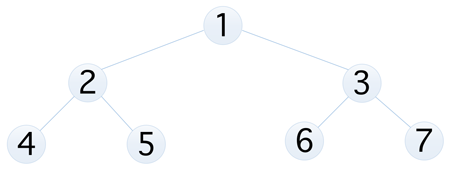
根据上图，我们可以很明显的看出它的特点

叶子结点只能出现在最下两层
最下层的叶子一定集中在左部连续位置（注意这里是左部）
倒数第二层，若有叶子结点，一定都在右部连续位置
如果结点度为一，则该结点只有左孩子
同样结点树的二叉树，完全二叉树的深度最小

这里特别需要注意的一点是，满二叉树『一定是』完全二叉树，但完全二叉树『不一定是』满二叉树，比如下面的一些情况，『均不是完全二叉树』

二叉树的性质

在了解完二叉树的一些基本概念以后，我们来看看二叉树的性质，按分类可以归纳为五类，我们一个一个来看

性质一

在二叉树的第 i 层上至多有 2 ^ (i - 1) 个结点（i >= 1），这个很好理解，参考上方的二叉树图例便很可以很快的推导出来

性质二

深度为 k 的二叉树至多有 2 ^ k - 1 个结点（k >= 1），这个同上，不过需要注意的是 k 次方以后在减去 1，而不是 k - 1 次方，注意与性质一区分开来

性质三

对任何一棵二叉树 T，如果其终端结点数为 n0，度为二的结点数为 n2，则 n0 = n2 + 1，这个理解起来稍微复杂一些，但是用的地方不多，了解一下即可，推导过程如下

首先我们再假设度为 1 的结点数为 n1，则二叉树 T 的结点总数 n = n0 + n1 + n2
其次我们发现连接数总是等于总结点数 n - 1，并且等于 n1 + 2 * n2
所以 n - 1 = n1 + 2 * n2
所以 n0 + n1 + n2 - 1 = n1 + n2 + n2
最后两边减去相同项，得出 n0 = n2 + 1

性质四

具有 n 个结点的完全二叉树的深度为 ⌊log₂n⌋ + 1，这个同上，一般使用的也不是很多，了解即可，但是这里需要注意的就是这一对符号，⌈...⌉ 表示向上取整（上有起止，开口向下），而 ⌊...⌋ 则表示向下取整（下有起止，开口向上），下面我们来看看推导过程

由性质二我们可知，深度为 k 的满二叉树的结点树 n 一定是 2 ^ k - 1
那么对于满二叉树我们可以通过 n = 2 ^ k - 1 倒推得到满二叉树的深度为 k = log₂(n + 1)
由于完全二叉树前边我们已经提到，它的叶子结点只会出现在最下面的两层，那么对于倒数第二层的满二叉树我们同样很容易回推出它的结点数为 n = 2 ^ (k - 1) - 1
所以完全二叉树的结点数的取值范围是 2 ^ (k - 1) -1 < n <= 2 ^ k - 1
由于 n 是整数，所以 n <= 2 ^ k - 1 可以看成 n < 2 ^ k
同理 2 ^ (k - 1) - 1 < n 可以看成 2 ^ (k - 1) <= n，所以 2 ^ (k - 1) <= n < 2 ^ k
不等式两边同时取对数，得到 k - 1 <= log₂n < k
由于 k 是深度，必须取整，所以 k = ⌊log₂n⌋ + 1

性质五

如果对一棵有 n 个结点的完全二叉树（其深度为 ⌊log₂n⌋ + 1）的结点按层序编号，对任一结点 i（1 <= i <= n）有以下性质

如果 i = 1，则结点 i 是二叉树的根，无双亲，如果 i > 1，则其双亲是结点 ⌊i / 2⌋（比如 6 和 7 结点的双亲结点为 3）
如果 2i > n，则结点 i 无做左孩子（结点 i 为叶子结点），否则其左孩子是结点 2i（还是以结点 6 为例，2n = 12，如果总结点 n < 12，则表示结点 6 无左孩子，否则结点 6 的左孩子的结点为 12）
如果 2i + 1 > n，则结点 i 无右孩子，否则其右孩子是结点 2i + 1（同上，不过这次是奇数，对应着右侧）

二叉树的存储结构

在了解完二叉树的一些定义和性质以后，我们再来看看二叉树的存储结构，树结构在计算机中的存储形式很多，在前面的示例当中我们也可以发现，很难单单只用顺序存储结构或者链式存储结构来存放，但是二叉树是一种特殊的树，由于它的特殊性，使得用顺序存储结构或链式存储结构都能够简单实现

二叉树的顺序存储结构就是用一维数组存储二叉树中的各个结点，并且结点的存储位置能体现结点之间的逻辑关系，比如下图的这个二叉树，就可以直接使用数组来进行表示

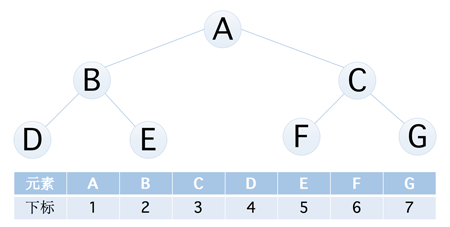
通过上面这个例子就可以看出完全二叉树的优越性，由于它的严格定义，所以我们就可以直接在数组当中表现出它的逻辑结构

二叉树的顺序存储结构

当然对于一般的二叉树，尽管层序编号不能反映逻辑关系，但是也可以按照完全二叉树编号方式修改一下，把不存在的结点用 ^（空指针 null）代替即可，如下图，虽然不是一个完全二叉树，但是依然可以使用数组来进行表示

但是我们要考虑到这样一种极端的情况，即如果是斜树，那么改如何表示呢？当然，通过上面的例子，你可能会说是下面这样的

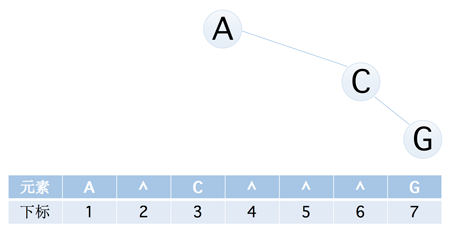
但是我们仅仅为了存储只有三个元素的斜树，却要使用八个长度的数组，这显而易见会造成很大的浪费，那么有没有什么更好的方式来解决这样的问题呢？答案是有的，就是我们下面将要介绍的二叉链表

二叉链表

既然顺序存储方式的适用性不强，那么我们就要考虑链式存储结构，二叉树的存储按照国际惯例来说一般也是采用链式存储结构的，二叉树每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域是比较自然的想法，我们称这样的链表叫做二叉链表，如下图所示，中间是我们的 data，左边是左孩子指针，右边则是右孩子指针

二叉链表的结点结构定义代码如下

typedef struct BiTNode {
  ElemType data;
  struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

如果用图来表示的话，就是下面这样的

# Essay

二叉树