
之所以有线索二叉树一说,那么肯定是因为普通的二叉树是存在一定缺陷的,那我们首先就来看看为什么需要线索二叉树呢?
为什么需要线索二叉树
像单链表一样,在开发过程当中当发现单链表已经无法满足我们设计的程序某些要求的时候,就发明了双向链表来弥补一样,线索二叉树也是在需求中被创造的,那么普通的二叉树到底有什么缺陷呢?其实简单来说,就是浪费空间和时间,下面我们就通过一个示例来详细了解一下,比如下面这个图
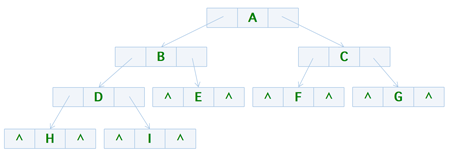
一眼看去可以发现有很多的 ^,也就是我们常说的空指针(null),这便是很明显的浪费行为,所以在这个过程当中,我们可以考虑利用 ^ 来记录该结点的前驱和后继,这样一来在查找过程当中,我们便可以快速的定位到某结点指定的前驱和后继结点,而不需要重新的整体遍历一遍
但是这时就会有一个问题了,我们在之前的 二叉树的遍历 章节当中已经了解到二叉树有多种遍历方式,不同的遍历方式都可以得到一个对应的遍历顺序,那么我们该以哪种遍历方式来进行遍历以达到可以节省 ^ 所浪费的空间呢?我们一个一个来进行尝试
前序遍历的方式
我们先来看看使用前序遍历的方式来遍历上图,它执行完以后的结果是 A ==> B ==> D ==> H ==> I ==> E ==> C ==> F ==> G,如果我们将存在 ^ 的结点标注为蓝色的话就是 A,B,D,H,I,E,C,F,G
通过观察我们可以发现,如果要把这些结点的 ^ 用来存储它们唯一的前驱和后继结点是不可行的,因为它们之间毫无规律可言
中序遍历的方式
下面我们再来考虑使用中序遍历的方式来看一下,它执行完以后的结果是 H ==> D ==> I ==> B ==> E ==> A ==> F ==> C ==> G,同样的,我们再来标注以下存在 ^ 的结点,结果为 H,D,I,B,E,A,F,C,G
这次我们发现它们是有规律的,即每隔一个结点,它刚好都有两个空余的 ^ 可以用来存放它的前驱和后继结点,所以我们就可以考虑使用中序遍历的方式来解决我们之前提到过的问题,如果按照中序遍历的方式来遍历之之前的问题,结果是下面这样的,图中的曲线表示该结点的前驱,直线表示该结点的后继,这样它们就可以串联起来了,所以我们可以通过定位一个结点从而快速的查找到它的前驱和后继结点
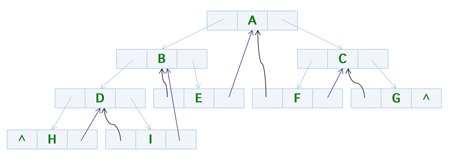
但是事情并没有那么简单,比如下面这个图,它并不是一个完全二叉树

我们还是按照中序遍历来进行标记一下,结果是 F,D,G,B,A,C,E
我们可以发现,标注为蓝色的结点还是具有空闲的指针位置,但是标记为绿色的结点却只有一个空闲的指针位置,如果是这样的话我们就面临一个问题,我们怎么去识别到底是存放指针还是线索呢?所以在这种情况下,我们可以将之前已经定义好的结构(二叉链表)稍微扩容一下,也就是变成下面这样

我们新增加了两个枚举类型的常量,ltag 和 rtag,这就是利用这两个常量来标识 lchild 和 rchild 是不是多余的空指针
ltag为0时指向该结点的左孩子(还原为本来的树),为1时指向该结点的前驱(线索)rtag为0时指向该结点的右孩子(还原为本来的树),为1时指向该结点的后继(线索)
遍历方式的对比
在上面我们使用了前序遍历和中序遍历的方式,至于其他的方式为什么没有使用,我们可以参考下面这个汇总的结果,对比一下三者之间的差别,图中实线表示指针,指向其左、右孩子,虚线表示线索,指向其直接前驱或直接后继
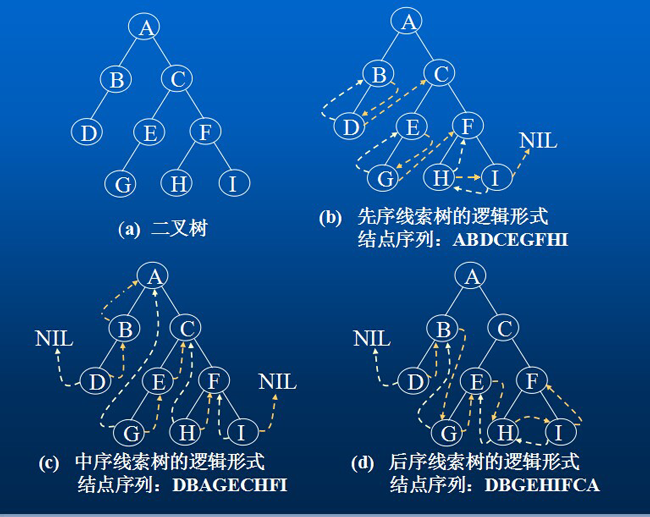
在线索树上进行遍历,只要先找到序列中的第一个结点,然后就可以依次找结点的直接后继结点直到后继为空为止,那么如何在线索树中找结点的直接前驱和后继呢?我们先来看如何在线索树中找结点的直接后继,以中序线索树为例
- 树中所有叶子结点的右链都是线索,右链直接指示了结点的直接后继
- 比如结点
G的直接后继是结点E
- 比如结点
- 树中所有非叶子结点的右链都是指针,根据中序遍历的规律,非叶子结点的直接后继是遍历其右子树时访问的第一个结点,即右子树中最左下的(叶子)结点
- 比如结点
C的直接后继查找顺序是先沿右指针找到右子树的根结点F,然后沿左链往下直到ltag = 1的结点即为C的直接后继结点H
- 比如结点
至于查找线索树中结点的直接前驱元素,若结点的 ltag = 1,则左链是线索,指示其直接前驱,否则在遍历左子树时访问的最后一个结点(即沿左子树中最右往下的结点)为其直接前驱结点,这里稍微提及一下,对于后序遍历的线索树中找结点的直接后继比较复杂,可分以下三种情况
- 若结点是二叉树的根结点,则其直接后继为空
- 若结点是其父结点的左孩子或右孩子且其父结点没有右子树,则直接后继为其父结点
- 若结点是其父结点的左孩子且其父结点有右子树,则直接后继是对其父结点的右子树按后序遍历的第一个结点
线索二叉树的定义
线索二叉树其实也就是二叉树的线索化,它指的是依照某种遍历次序使二叉树成为线索二叉树的过程,其实简单来说就是一般的二叉树,只不过在遍历的过程当中添加了线索化的过程,线索化的过程就是在遍历过程中修改空指针使其指向直接前驱或直接后继的过程,仿照线性表的存储结构,我们可以在二叉树的线索链表上也添加一个头结点 head,头结点的指针域的安排是
lchild域,指向二叉树的根结点rchild域,指向中序遍历时的最后一个结点- 二叉树中序序列中的第一个结点
lchild指针域和最后一个结点rchild指针域均指向头结点head
简单来说就是如同为二叉树建立了一个双向线索链表,对一棵线索二叉树既可从头结点也可从最后一个结点开始按寻找直接后继进行遍历,显然这种遍历不需要堆栈
线索二叉树的遍历
在线索二叉树中,由于有线索存在,在某些情况下可以方便地找到指定结点在某种遍历序列中的直接前驱或直接后继,此外,在线索二叉树上进行某种遍历比在一般的二叉树上进行这种遍历要容易得多,不需要设置堆栈,代码实现如下,不过一般使用较少,了解即可
1 | // 线索存储标志位 |




