
在上一章当中我们研究了 最短路径 的相关算法,它们是迪杰斯特拉算法(Dijkstra)和弗洛伊德算法(Floyd),本章我们就来了解一下关键路径的一些相关算法,这也是图结构相关内容的最后一部分,但是在展开之前,我们需要先来了解一些前置知识,它们就是『拓扑序列』和『拓扑排序』
拓扑序列
那么什么是拓扑序列呢?在前面的章节当中,我们已经知道,一个无环的有向图可以称之为无环图(Directed Acyclic Graph),我们可以将其简称为 DAG 图,而在一个表示工程的有向图中,如果用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图就称为顶点表示活动的网,我们称之为 AOV 网(Active On Vertex Network),而 AOV 网中的弧表示活动之间存在的某种制约关系,简单来说就说 AOV 网不能存在回路
这里涉及到几个新的概念,比如工程和活动,我们可以这样来进行理解
比如你想要开一家店铺,那么开店铺这整个流程,我们就可以将其称之为一个工程,而开店铺过程当中涉及到的比如选址,装修,进货等行为,我们就可以将其称之为一个一个的活动,所有的工程或者某种流程都可以分为若干个小的工程或者阶段,我们称这些小的工程或阶段为活动,而至于不能存在回路,可以理解为你不能先进行装修和进货,而是必须要在店铺的选址工作完成了以后才能进行接下来的流程,这样一来是不是就比较容易理解了,下面我们在来看看拓扑排序
拓扑排序
之前我们介绍的拓扑序列,如果使用概念来进行定义的话,是这样的
设
G = (V, E)是一个具有n个顶点的有向图,V中的顶点序列V1, V2, ... Vn满足若从顶点Vi到Vj有一条路径,则在顶点序列中顶点Vi必在顶点Vj之前,则我们称这样的顶点序列为一个拓扑序列
而所谓的拓扑排序,其实就是对一个『有向图构造拓扑序列』的过程,我们可以以一个具体的例子来进行理解,如下图
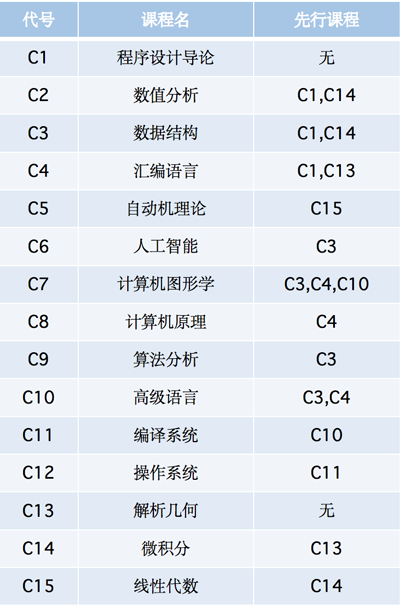
上图是某校计算机专业所修课程,比如代号 C1 的课程,它就不需要前置课程,而比如对于课程 C3 它就需要 C1 和 C14 这两门前置课程,我们将上图转换为 AOV 网是下面这样的
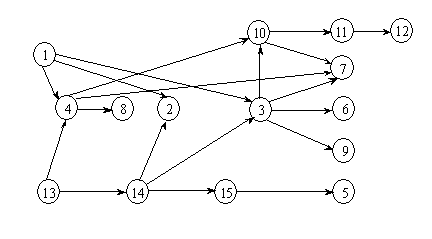
针对于上图其中的一种拓扑序列为 1, 13, 4, 8, 14, 15, 5, 2, 3, 10, 11, 12, 7, 6, 9(在下面我们会通过代码来进行求解),在用代码实现之前,我们先来看看针对 AOV 网进行拓扑排序的方法和步骤,主要流程如下,主要利用了栈的特点
- 从
AOV网中选择一个没有前趋的顶点(该顶点的入度为0)并且输出它 - 从网中删去该顶点,并且删去从该顶点发出的全部有向边
- 重复上述两步,直到剩余网中不再存在没有前趋的顶点为止
有了实现步骤,下面我们就来看看如何使用代码来进行实现,由于需要删除顶点,所以在这里我们选择『邻接表』的数据结构来表示会更加方便(相较于邻边矩阵),形式如下
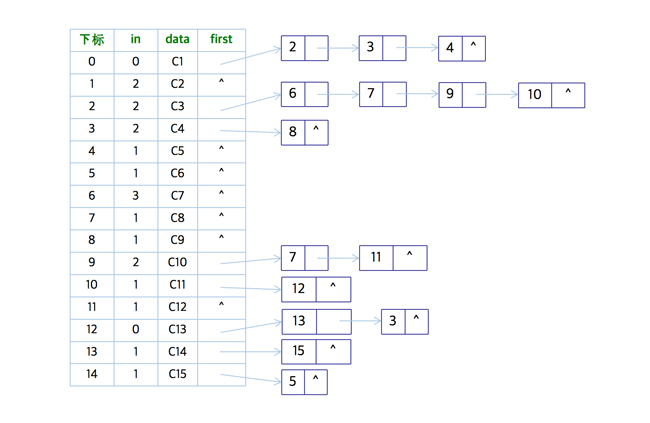
针对于该算法时间复杂度而言
- 对一个具有
n个顶点,e条边的网来说,初始建立入度为零的顶点栈,要检查所有顶点一次,执行时间为O(n) - 排序中,若
AOV网无回路,则每个顶点入、出栈各一次,每个表结点被检查一次,因而执行时间是O(n + e) - 所以,整个算法的时间复杂度是
O(n + e)
首先我们需要先来生成图
1 | class vex { |
当有了图以后,我们就可以来实现我们的排序操作
1 | function topoSort(G) { |
关键路径的作用
在了解完拓扑排序以后,我们就可以正式的来看看关键路径,不过对于一个新东西,在了解它之前我们一般都会先了解它是做什么的,它解决了什么样的问题,同样的,我们也使用一个示例来进行说明
比如某汽车公司生产一辆汽车,其中生产轮子需要 0.5 天,发动机需要 3 天,底盘需要 2 天,外壳需要 2 天,其他零部件需要 2 天,全部零部件集中到一处需要 0.5 天,组装成车并测试需要 2 天,那么请问生成一辆汽车最短需要多少时间呢?
针对于上面这个例子,通过简单的计算就可以得出结果,但是如果是在实际当中,往往会涉及到其他更多的部门分工合作,所以也就会变得更为复杂,那么针对于这种情况,我们该如何处理这样的问题呢?所以这就有了我们的关键路径算法,它的定义是下面这样的
在一个表示工程的带权有向图(注意这里是带权的)中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间,这种有向图的边表示活动的网,我们称之为
AOE网(Activity On Edge Network)
我们把 AOE 网中没有『入边』的顶点称为始点或源点,没有『出边』的顶点称为终点或汇点,如下图所示
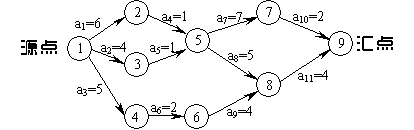
AOV 网与 AOE 网的比较
下面我们来看看两者之间的区别,有一个比较好的记忆方式就是,注意它们是否带权,不带权的就是 AOV,而带权的就是 AOE,如下
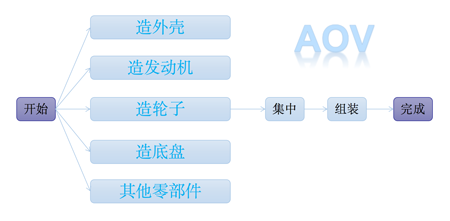
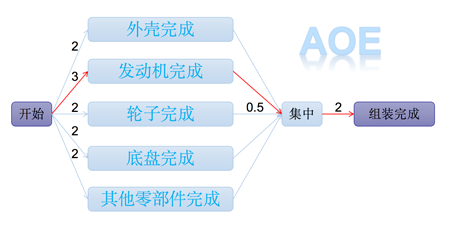
而像上图 AOE 网当中标注的红色路线就是我们的关键路径,下面我们就来看看关键路径是如何建立在拓扑序列之上的
关键路径
简单来说,关键路径的算法就是我们先求得顶点事件的最早和最晚发生时间,再求得弧活动的最早和最晚开工时间,最后比较弧活动的两者时间是否相等,然后判断其是否为关键活动,在这里涉及到了四个新的概念,我们先来了解一下
| 名词 | 定义 |
|---|---|
etv |
事件的最早发生时间,就是顶点的最早发生时间,简单来说就是 源点 ==> 汇点 |
ltv |
事件的最晚发生时间,就是每个顶点对应的事件最晚需要开始的时间,如果超出此时间将会延误整个工期,简单来说就是 汇点 ==> 源点 |
ete |
活动的最早开工时间,就是弧的最早发生时间 |
lte |
活动的最晚开工时间,不推迟工期的最晚开工时间 |
其实简单来说,关键路径就是『源点到汇点之间权值最大的一条路径』,这条路径决定了整个工期,关键路径上的关键活动的最早开始的时间和最晚开始的时间应该是相同的(也就是 etv == ltv),否则说明还有其他工程会影响工期,这条路径就不是关键路径了,而引入 ete 和 lte 是为了通过循环边来找出关键活动,同时可以得到边上的权,还是以下图为例

根据图中的信息,我们可以得到如下信息
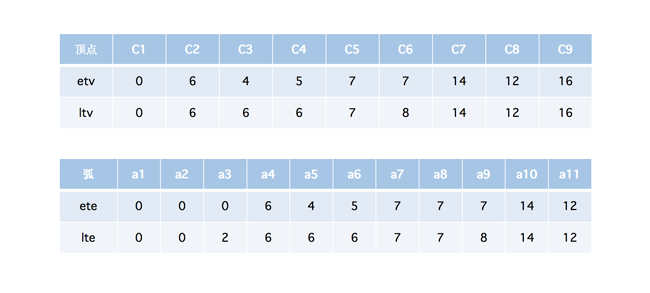
下面来简单介绍一下上图中的信息
- 顶点我们就使用
C1,C2 ... C9来进行表示,左边是源点,右边是汇点 etv,事件的最早发生时间,也就是从左往右,比如C2这个点,它需要经过a1这个活动结束以后才能到达C2,所以C2的值为6,这里我们主要看一下C5这种情况,它需要等两条线路都结束以后才能开始,所以它的值为7,其他的点都是同理ltv,事件的最晚发生时间,我们这里是从右往左,整个工程所需要的时间是16个单位,因为a11执行需要四个单位,所以C8所需要的最迟时间也就是12,这里我们主要看一下C6的情况,因为a9需要4个单位,所以C6的值是8(这里需要注意的就是ltv的C1是取的较小的值,也就是这里的0),所以在C6这个点上我们可以发现,它最早发生的时间是7,而最晚发生的时间是8,它们之间是相差一个单位的ete,活动的最早开工时间,我们可以发现,我们有9个顶点,但是却产生了11条弧,比如a1,a2,a3它们的事件都是从C1开始的,所以它们都是0,我们来看a4这条弧,它对应着C2最早的发生时间,通过观察可知,C2的etv的值为6,所以它的ete的值也为6,同理,a5就相当于C3的最早发生时间,是不是有点眉目了,后面都是以此类推lte,活动的最晚开工时间,又是最晚,所以我们需要从右往左来看,简单来说比如a9这条弧,对应着C8这个点的ltv,它的ltv的值为12,所以a9为12 - 4 = 8
所以简单的总结一下就是,如果得出了 etv 和 ltv 的值以后,就可以很简单的推算出 ete 和 lte 的值了
etv可以直接推断出ete- 而
lte可以简单的换算得到ltv
这里有一个需要注意的地方,就是如果细心观察可以发现,图上的 C1,C2,C5 ... 等点,也就是下图这些点

它们的 etv 是等于 ltv 的,通过图我们可以发现,其实它们之间的连线也就是我们所要的关键路径,但是这里存在一个问题,既然知道连接弧就是关键路径,那么为什么还有必要要求得 ete 和 lte 呢
首先,关键路径是活动的集合,也就是弧的集合而不是事件的集合,虽然我们可以求出 etv == ltv 的情况,也可以一眼就看出结果,但是对于计算机而言,我们还是需要让它通过弧将其表现出来的,况且有了 etv 和 ltv,通过我们上面的介绍,得出 ete 和 lte 也是十分简单的
代码实现
其实通过上面的内容,我们可以将整个求解关键路径的过程划分为三部分
- 求解各顶点事件的最早发生时间
- 求解各顶点事件的最晚发生时间
- 求解各弧上活动的最早和最晚发生时间,并做关键活动的判断
邻边表如下,右侧加粗的部分表示权值
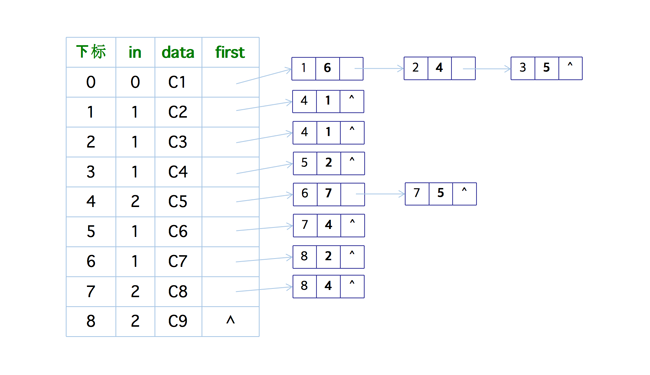
我们还是在我们之前的拓扑排序的基础之上来进行调整,首先求得各顶点事件的最早发生时间,可以与拓扑排序相对比,可以发现它们是很相似的
1 | function getEtvs(G) { |
接着根据各顶点事件的最早发生时间,反向求各顶点的最晚发生时间,相当于把拓扑排序倒过来
1 | function getLtvs(G, etvs, T) { |
最后即可根据各顶点事件的最早和最晚发生时间,计算弧上活动的最早和最晚时间,并作比较判断是否为关键活动,需要注意的是,弧上活动 <Vi, Vj> 的最早开工时间不可能早于顶点 Vi 事件最早发生时间,而最晚开工时间则不可能晚于顶点 Vj 事件最晚发生时间减去弧上活动持续时间
1 | function criticalPath(G) { |




