我们在上一章的 查找算法 当中介绍了算法的分类和一些比较常用的算法,比如二分,插值等等,但是它们的使用都需要一个前提条件,那就是『元素必须是有序的』,那么如果对于无序列表,我们又需要怎么来进行处理呢?这也就是我们今天将要介绍到的『二叉排序树』
为什么需要二叉排序树
这里既然提到了二叉排序树,那我们就先来看看为何需要『二叉排序树』?针对于无序序列,比如我们的顺序存储结构,我们都知道,如果需要删除其中的一个元素,那么我们首先应该取出删除元素,然后从删除元素位置开始遍历到最后一个元素位置,分别将他们都向前移动一个位置,可想而知,这样的操作的效率是十分低下的,如下所示
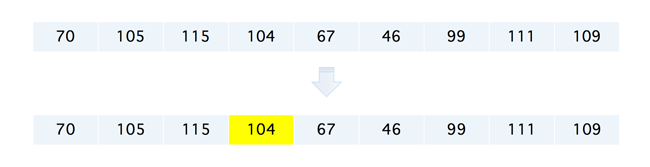
比如我们想要删除掉 104 这个元素,那么在将它删除掉了以后,它后面所有掉元素都需要向前移动一个位置,以保证存储结构的完整,当然也有说那是不是可以换一种删除方式呢,方法的确有很多种,比如下面这种
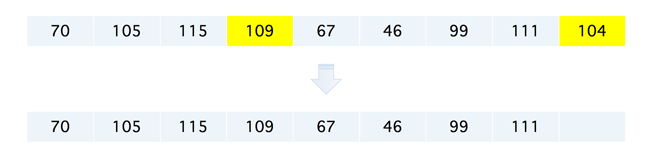
我们将待删除的 104 和末尾的 109 互换位置,然后将结构的长度缩减一位也可以达到我们的目的,虽然可以达到我们的目的,但是由于这样的序列它是无序的,所以就造成查找的效率很低,那么有没有一种插入和删除的效率还不错,又可以高效率查找的算法呢,那就是我们下面将要介绍的『二叉排序树』
二叉排序树
在之前的章节当中,我们曾经介绍过了 二叉树的的定义 和 二叉树的遍历,但是在之前的内容当中我们并没有涉及到针对二叉树的一些查找和删除等操作,仅仅只是涉及到了遍历和插入操作,那么在今天我们就来看看如何在二叉树当中进行查找和删除等操作,不过在展开之前,我们需要先来了解一下,什么是二叉排序树呢?我们先来看下面这个图

我们可以考虑将这个数据集排列成二叉树的方式,但是做一点小小的约束,我们约定『它只允许在左结点存储比父结点更小的值,右结点存储比父结点更大的值』,依照这个原则,我们就有了下面这个二叉树
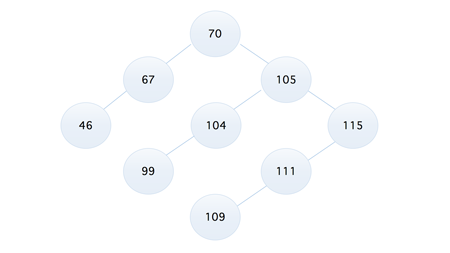
上面这个图就可以称之为二叉排序树,二叉排序树(Binary Sort Tree)又称为『二叉查找树』,它是一棵空树,或者是具有下列性质的二叉树
- 若它的左子树不为空,则左子树上所有结点的值均小于它的根结构的值
- 若它的右子树不为空,则右子树上所有结点的值均大于它的根结构的值
- 它的左、右子树也分别为二叉排序树(递归)
它既然被称为排序树,那么肯定是与排序有关的,比如针对上面这个例子,如果我们采用中序遍历的方式,我们就可以得到一个从小到大排好顺序的一个序列,也就是说我们存储的数据,虽然它是无序的,但是如果按照二叉排序树的方式来进行存储,那么我们只需要通过中序遍历的方式就可以得到一个有序的序列,但是我们构造这么一个二叉排序树的目的不单单只是为了排序这么简单,而是为了提高查找,插入和删除的效率
查找
下面我们就来看看如何在二叉排序树当中进行查找操作,原理同插入操作是类似的,本质上都是利用递归来进行的,这个方法首先会检验 node 的合法性,如果为 null,直接退出,并返回 fasle,如果传入的 key 比当前传入 node 的 key 值小,它会继续递归查找 node 的左侧结点,反之,查找右侧结点,如果找到相等结点,直接退出,并返回 true
下面我们就来看看如何实现,代码如下,也就是在我们之前的 二叉树的建立 的基础上进行扩充
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
find(key) {
var node = this.root
while (node != null) {
if (key < node.key) {
node = node.left
} else if (key > node.key) {
node = node.right
} else {
return node
}
}
return null
}
|
在这里我们多看一步,那就是如何查找最小、最大值呢?其实也很简单,其实在之前二叉树的建立的部分我们也略微提及过,那就是查找二叉树的最小值和最大值就是二叉树左右两侧最边缘部分的那个结点(最左侧或者最右侧),我们只需要将根节点传入 minNode 或 maxNode 方法,然后通过循环判断 node 是否为最左侧或者最右侧的节点(如果是的话,此时的值是为 null 的),下面我们来看看如何实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
getMin(node) {
node = node || this.root
while (node.left != null) {
node = node.left
}
return node.key
}
getMax(node) {
node = node || this.root
while (node.right != null) {
node = node.right
}
return node.key
}
|
删除
最后我们再来看最为复杂的情况,那就是删除结点,我们可以对照下图来看,一一捋清楚它的各种情况

按照移除的方式不同,我们可以大致将其分为三种情况
- 需要移除的节点是一个叶子节点(比如上面的
46,99 等),这种情况下,直接删除就可以了,因为它不会对整颗二叉排序树的特点造成影响
- 需要移除的节点仅有一个子节点(只有左子树或者右子树),这种情况也直接删除,然后将其的左子树或者右子树连接到它的双亲那里就可以了(比如直接删掉
67,然后将它的左子树 46 连接到 70 即可)
- 需要移除的节点包含两个子节点(也就是最为复杂的情况,既有左子树又有右子树的情况),我们这里比如需要删除
105,按照我们的中序遍历方式来看的话,那么替代它的最好的就是它的直接前驱或者后继,也就是 104 或者 108
- 所以如果直接删除
105 的话,可以使用 104 来顶替它的位置,而 103 来顶替 104 的位置
- 如果使用
108 来顶替的话,同样的道理,如果 108 存在右子树的话,只需要将其连接到 110 的左子树上即可
- 因为
108 大于 105 的所有左子树,同理 104 也是小于 115 所有的左子树
- 有一个需要注意的就是,
104 是不会存在右子树的,如果存在则需要替换的目标就是它的右子树了,而不会是 104(同理 108 也不会存在左子树)
下面来看代码如何实现,其中,也就是移除包含两个子节点的节点是最复杂的情况,它包含左侧节点和右侧节点,对它进行移除主要需要三个步骤
- 需要找到它右侧子树中的最小节点来代替它的位置
- 将它右侧子树中的最小节点移除
- 将更新后的节点的引用指向原节点的父节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
remove(key) {
this.root = this.removeNode(this.root, key)
}
removeNode(node, key) {
if (node == null) {
return null
}
if (key < node.key) {
node.left = this.removeNode(node.left, key)
return node
} else if (key > node.key) {
node.right = this.removeNode(node.right, key)
return node
} else {
if (node.left == null && node.right == null) {
node = null
return node
} else if (node.left == null) {
return node.right
} else if (node.right == null) {
return node.left
} else {
var minNode = this.getMin(node.right)
node.key = minNode.key
node.right = this.removeNode(node.right, minNode.key)
return node
}
}
}
|
完整代码
下面是整合以后的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
| class Node {
constructor(key) {
this.key = key
this.left = null
this.right = null
}
}
class BinaryTree {
constructor() {
this.root = null
}
insert(key) {
var newNode = new Node(key)
if (this.root == null) {
this.root = newNode
} else {
var current = this.root
while (true) {
if (key < current.key) {
if (current.left) {
current = current.left
} else {
current.left = newNode
break
}
} else if (key > current.key) {
if (current.right) {
current = current.right
} else {
current.right = newNode
break
}
}
}
}
}
centerSort(node) {
if (node) {
this.centerSort(node.left)
console.log(node.key)
this.centerSort(node.right)
}
}
prevSort(node) {
if (node) {
console.log(node.key)
this.prevSort(node.left)
this.prevSort(node.right)
}
}
nextSort(node) {
if (node) {
this.nextSort(node.left)
this.nextSort(node.right)
console.log(node.key)
}
}
getMin(node) {
node = node || this.root
while (node.left != null) {
node = node.left
}
return node.key
}
getMax(node) {
node = node || this.root
while (node.right != null) {
node = node.right
}
return node.key
}
find(key) {
var node = this.root
while (node != null) {
if (key < node.key) {
node = node.left
} else if (key > node.key) {
node = node.right
} else {
return node
}
}
return null
}
remove(key) {
this.root = this.removeNode(this.root, key)
}
removeNode(node, key) {
if (node == null) {
return null
}
if (key < node.key) {
node.left = this.removeNode(node.left, key)
return node
} else if (key > node.key) {
node.right = this.removeNode(node.right, key)
return node
} else {
if (node.left == null && node.right == null) {
node = null
return node
} else if (node.left == null) {
return node.right
} else if (node.right == null) {
return node.left
} else {
var minNode = this.getMin(node.right)
node.key = minNode.key
node.right = this.removeNode(node.right, minNode.key)
return node
}
}
}
}
|










