在上一节当中,我们介绍了 二叉排序树 以及它的查找和删除等操作,但是它其实是存在一定问题的,至于到底是什么问题,下面我们慢慢来看
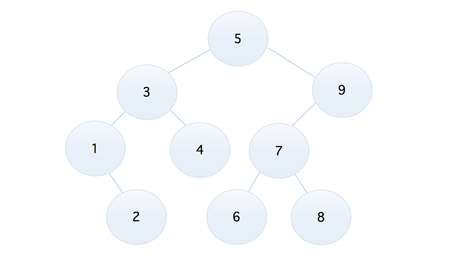
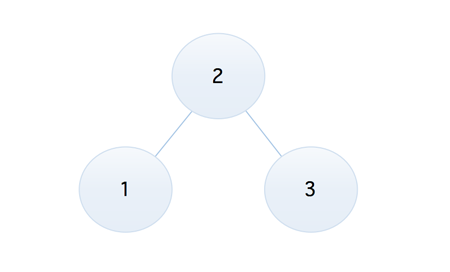
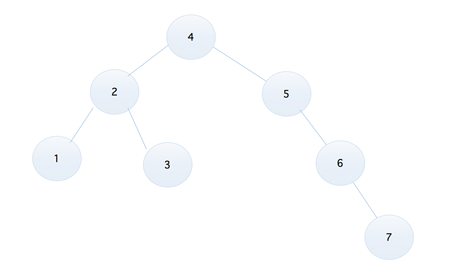
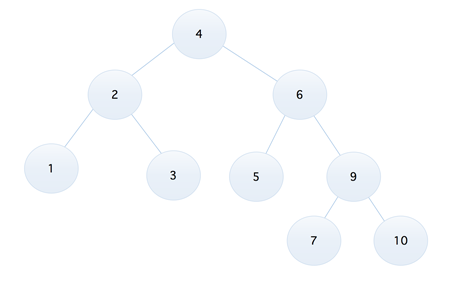
二叉排序树存在的问题 比如我们现在有这样一个序列,5, 9, 3, 7, 1, 4, 6, 8, 2,将它转换为二叉排序树,是下面这个样子的
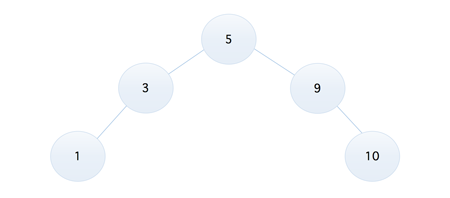
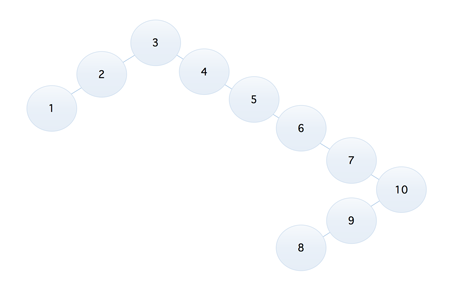
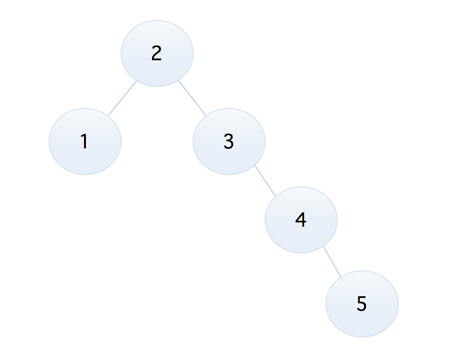
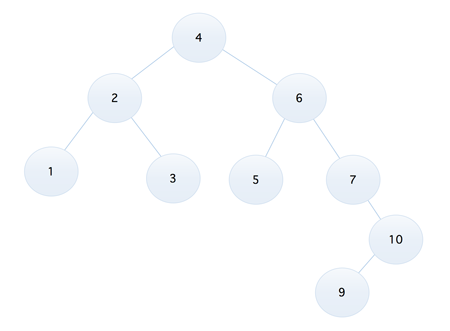
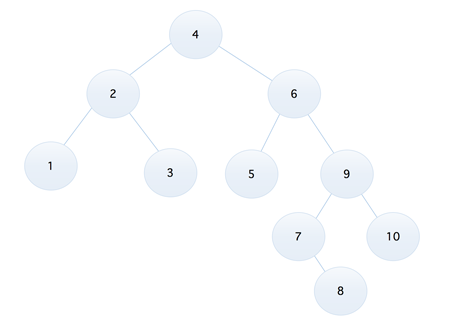
看上去还不错的样子,比如我们要查找 9 这个元素,两次对比后就可以得到结果,但是如果我们将序列调整为 1, 2, 3, 4, 5, 6, 7, 8, 9,那么它就成了下面这样的
可以发现,此时竟然成为了一颗右斜树,但是它的确也是一颗二叉排序树,而如果这时如果我们再去查找 9 这个元素的话,效率可想而知,所以我们可以发现,不同的二叉树,它的查找效率是不一样的,所以我们就需要想办法找到一个合适的方式,不管提供的序列是什么样子的,都可以生成一个查找效率尽量高的二叉排序树,那就是我们下面将要介绍的『平衡二叉排序树』(AVL 树)
平衡二叉排序树 由名字就可以知道,我们的平衡二叉排序树它是一颗高度平衡的二叉树,意思就是要么它是一颗空树,要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值『不超过一』
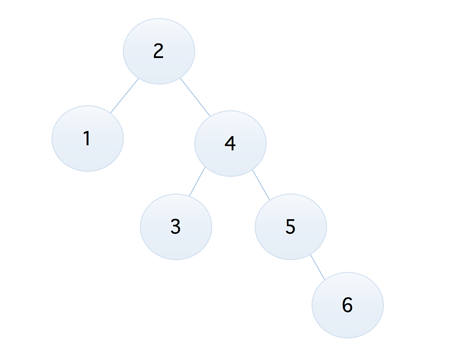
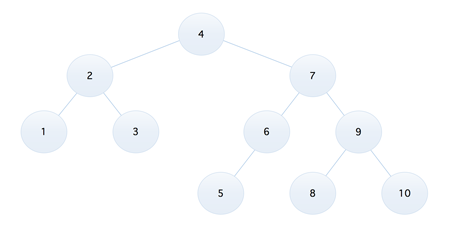
用官方的话来进行描述就是,我们将二叉树上的结点上的左子树的深度的值减去右子树的深度的值称为『平衡因子 BF』(BalanceFactor),平衡二叉树就是一棵二叉树上所有结点的平衡因子的绝对值小于等于 1 的树(所以它只有三个值,1,0,-1),比如下面这个就是『平衡二叉排序树』
而下面这个就不符合条件,因为平衡二叉排序树首先要是一棵树,接着需要是一颗二叉排序树,下面这个明显不符合二叉排序树的概念
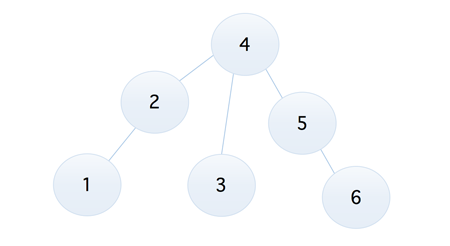
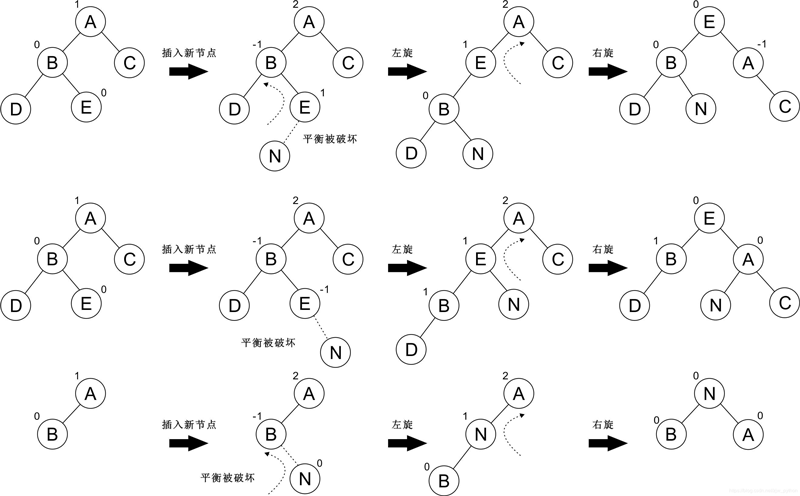
在来看下面这个例子
它其实也不是平衡二叉排序树,因为比如结点 9,它的左子树和右子树的差的绝对值已经大于 1 了,再来看最后一个图
它就是一颗平衡二叉排序树了
平衡二叉排序树的构建过程 下面我们来看平衡二叉排序树是如何一步一步构建出来的,我们以序列 3, 2, 1, 4, 5, 6, 7, 10, 9, 8 为例,它构造出来的二叉排序树是下面这样的
让我们抛开上图,一步一步从头开始进行操作,首先是根结点 3,和它的两个左子树元素 2 和 1,那么就会是下面这样的
可以发现,这个时候就已经存在问题了,因为结点 3 的平衡因子已经为 2 了(2 - 0 = 2),所以在插入结点 1 的时候我们就应该来适当的进行调整,调整的方式为『如果平衡因子是正数,且大于 1,那么对应的整颗子树就对应的向右进行旋转(顺时针)』,就变成来下面这样
下面我们在继续来进行添加,我们在依次插入结点 4 和 5,如下
此时又出现问题了,3 的平衡因子为 -2,而又是因为它的不平衡连带导致现在的根结点 2 也不平衡了,所以我们需要来对结点 3 进行处理,调整的方式为『如果平衡因子是负数,并且小于 -1,那么对应的整颗子树就对应的向左进行旋转(逆时针)』,所以就成了下面这样
下面我们继续操作,插入结点 6,变成了下面这样
这时可以发现,4,5,6 都是符合的,但是结点 2 却不符合了,所以我们此时需要调整结点 2,可以发现它的平衡因子是负数,所以左旋转,也就成了下面这样
但是此时可以发现,旋转以后作为新的根结点的 4,它有三个子结点了,这明显不符合我们二叉树的原理的,所以此时我们就需要针对结点 3 来进行处理,因为我们之前曾经提到过,一个结点的右子树的最左边的那个孩子,事实上可以放在这个结点的左子树的最右边的孩子位置,所以就变成了下面这样,此时又变成了平衡二叉树
下面继续插入结点 7,如下
老规矩,发现结点 5 的平衡因子为 -2,所以左转,就变成了下面这样
继续插入结点 10 和 9
又发现问题,结点 9 的插入导致了结点 4,6,7 的 BF 值均为 -2,但是这里注意,结点 10 的 BF 是为 1 的,所以这时如果按照我们之前的逻辑,负数向左旋转,我们可以尝试一下来调整结点 7,结果如下
这下发现麻烦大了,结点 9 竟然成为了结点 10 的右孩子,所以我们的尝试是不对的,因为我们可以注意,在之前的情况当中的 BF 值要么全部为正,要么全部为负,而这一次的情况是有正也有负,所以我们需要针对这种特殊的情况来单独进行处理,所以这里,我们需要按照步骤来走,先来处理结点 10,因为它的 BF 为正,所以向右旋转,就变成了下面这样
此时的 BF 就全部为负了,我们在按照我们之前的逻辑来处理结点 7,也就是向左旋转,就得到了下面这样
这时发现就是平衡的了,所以可以再次插入我们最后的结点 8,如下
这时可以发现,结点 4,6 的 BF 都为 -2,而结点 9 的 BF 却是为 1 的,所以按照我们之前的逻辑需要先将结点 9 进行右转,然后此时的 BF 值就统一成负数了,这时在进行左转就得到了我们的最终结果,这里也就直接跳过了,逻辑与上方是一样的,最后可以得到下面这样的结果
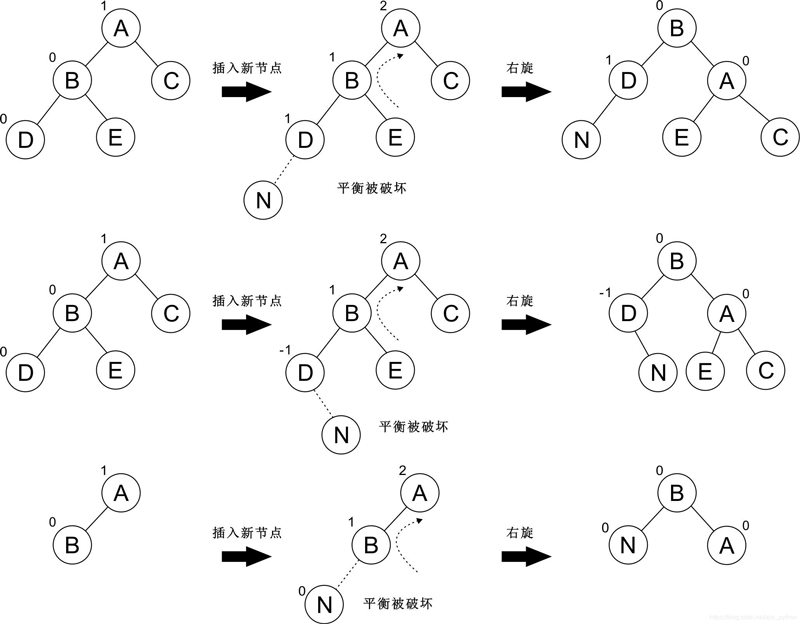
平衡二叉排序树的旋转 上面看完了流程,下面我们来大致的总结一下,其实简单来说,平衡二叉树的构建过程基于二叉排序树的构建过程,不过只是在插入节点的过程中,一旦出现不平衡现象(即某节点的平衡因子大于 1 或小于 -1),就找出最小不平衡子树,进行『旋转』操作,调整最小不平衡子树中各节点的链接关系,使之成为新的平衡子树
在二叉排序树中插入节点而失去平衡的情况下,对最小不平衡子树进行调整,总共有四种『旋转』类型(LL 型,RR 型,LR 型,RL 型),分别对应不同的不平衡情况,其中 LL 型和 RR 型只需要一次旋转,而 LR 型和 RL 型则需要两次旋转,每种类型又可进一步细分为三种情况,总共 4 × 3 = 12 种情况,具体如下图所示
LL 型 最小不平衡子树的根结点平衡因子值大于 1 且与根结点左孩子节点的平衡因子符号相同
RR 型 最小不平衡子树的根结点平衡因子值小于 -1 且与根结点右孩子节点的平衡因子符号相同
LR 型 最小不平衡子树的根结点平衡因子值大于 1 且与根结点左孩子节点的平衡因子符号不相同
RL 型 最小不平衡子树的根结点平衡因子值小于 -1 且与根结点右孩子节点的平衡因子符号不相同)
代码实现 本质上与我们的排序二叉树的实现方式类似,只不过多了一个平衡因子的参数,首先建立二叉树节点进行定义
1 2 3 4 5 6 constructor (num) { this .value = num this .height = 1 this .leftChild = null this .rightChild = null }
下面是整合后的代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 class AVLTree constructor (num) { this .value = num this .height = 1 this .leftChild = null this .rightChild = null } addNum(num) { let result = this let point = new AVLTree(num) if (point.value > this .value) { if (this .rightChild == null ) { this .rightChild = point } else { result.rightChild = this .rightChild.addNum(num) } let balanceFactor = this .getBalance(this .rightChild, this .leftChild) if (balanceFactor == 2 ) { if (point.value > this .rightChild.value) { result = this .RR() } else { result = this .RL() } } } else if (point.value < this .value) { if (this .leftChild == null ) { this .leftChild = point } else { result.leftChild = this .leftChild.addNum(num) } let balanceFactor = this .getBalance(this .leftChild, this .rightChild) if (balanceFactor == 2 ) { if (point.value < this .leftChild.value) { result = this .LL() } else { result = this .LR() } } } else { throw '输入了重复的值' } this .height = this .getMax(this .leftChild, this .rightChild) + 1 return result } deleteNum(num) { var result = this if (num > this .value) { result.rightChild = this .rightChild.deleteNum(num) } else if (num < this .value) { result.leftChild = this .leftChild.deleteNum(num) } else { if (num !== this .value) { throw '输入了没有的值' } if (result.leftChild !== null ) { let current = result.leftChild while (true ) { if (current.rightChild) { current = current.rightChild } else { break } } result.value = current.value result.leftChild = result.leftChild.deleteNum(current.value) } else if (result.rightChild !== null ) { let current = result.rightChild while (true ) { if (current.leftChild) { current = current.leftChild } else { break } } result.value = current.value result.rightChild = result.rightChild.deleteNum(current.value) } else { console .log('delete' + result) return null } } if (result.getBalance(result.leftChild, result.rightChild) == 2 ) { if (result.getHeight(result.leftChild.rightChild) - result.getHeight(result.leftChild.leftChild) == 1 ) { result = result.LR() } else { result = result.LL() } } else if (result.getBalance(result.leftChild, result.rightChild) == -2 ) { if (result.getHeight(result.rightChild.leftChild) - result.getHeight(result.rightChild.rightChild) == 1 ) { result = result.RL() } else { result = result.RR() } } else { console .log('is balance' ) } result.height = this .getMax(this .leftChild, this .rightChild) + 1 return result } getMax(a, b) { let aHeight, bHeight if (!a) { aHeight = 0 } else { aHeight = a.height } if (!b) { bHeight = 0 } else { bHeight = b.height } return aHeight > bHeight ? aHeight : bHeight } getBalance(a, b) { let aValue, bValue if (!a) { aValue = 0 } else { aValue = a.height } if (!b) { bValue = 0 } else { bValue = b.height } return aValue - bValue } getHeight(a) { if (a) { return a.height } return 0 } RR() { let a = this let b = this .rightChild a.rightChild = b.leftChild b.leftChild = a a.height = a.getMax(a.rightChild, a.leftChild) + 1 b.height = b.getMax(b.rightChild, b.rightChild) + 1 return b } RL() { let a = this a.rightChild = a.rightChild.LL() a = a.RR() return a } LL() { let a = this let b = this .leftChild a.leftChild = b.rightChild b.rightChild = a a.height = a.getMax(a.rightChild, a.leftChild) + 1 b.height = b.getMax(b.rightChild, b.rightChild) + 1 return b } LR() { let a = this a.leftChild = a.leftChild.RR() a = a.LL() return a } } function createTree (arr ) let result arr.forEach((child, index ) => { if (index === 0 ) { result = new AVLTree(child) } else { result = result.addNum(child) } }) return result } var arr = [1 , 3 , 5 , 7 , 15 , 24 , 56 , 11 , 33 , 42 , 2 , 4 , 6 , 12 ]var tree = createTree(arr)