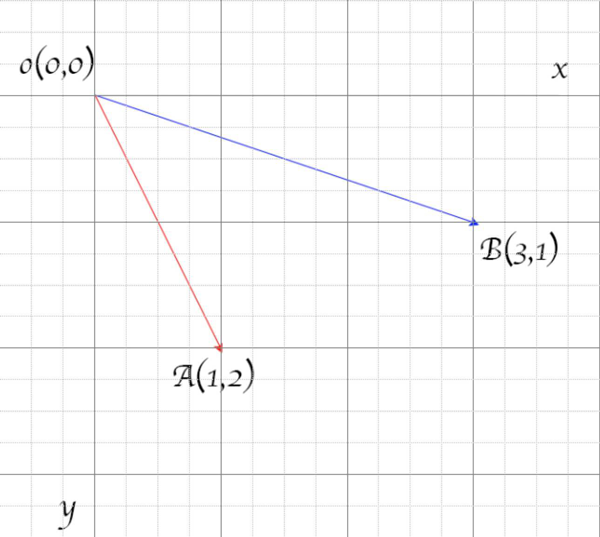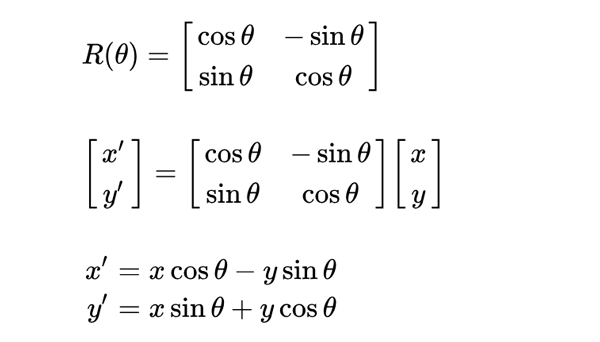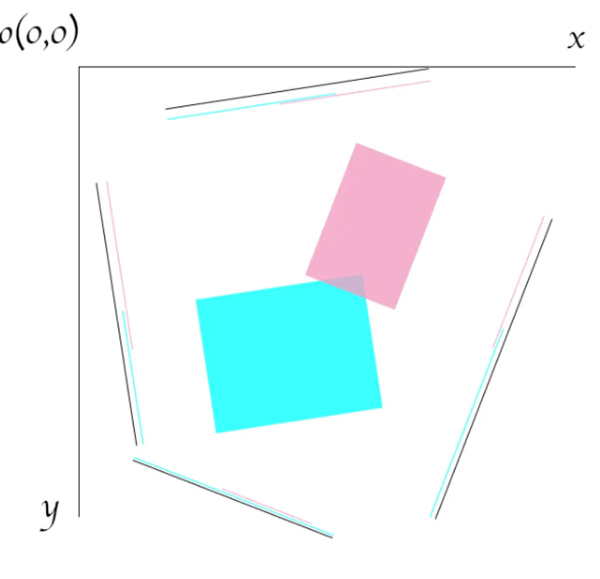2020-11-28

Essay

22 分钟读完 (大约 3242 个字)

矩形包围盒碰撞检测

最近在项目当中遇到一个需求，也是一个我们平常十分常见的操作，那就是框选操作，但是对于正常元素来说，我们只需要计算框选框是否包裹了当前的目标元素就可以知道当前元素是否选中，但是项目中的元素会存在旋转的情况，所以计算起来就会有些复杂了，所以就抽了些时间深入的了解了一下，也在这里记录记录

最终代码可见转向包围盒（OBB）这个在线示例

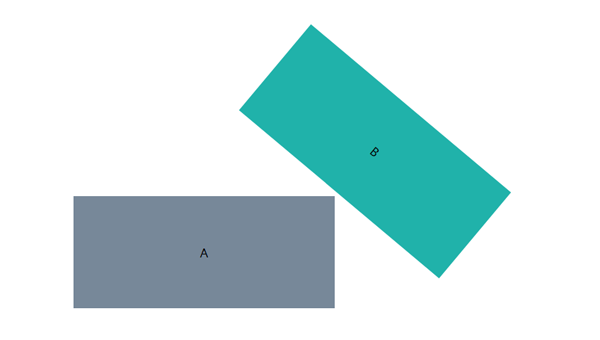
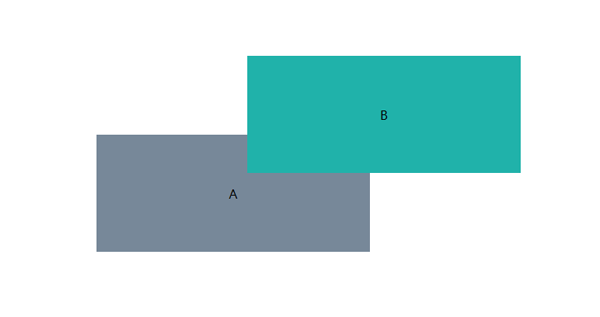
问题由来

需求如下，也就是我们平常接触到的框选操作，但是元素可能是旋转的，可以如下图所示

如上图，A 元素我们可以认为是鼠标操作生成的拖拽框，B 元素是我们的目标元素，问题就是如何判断当前 A 元素与 B 元素是否相交，周末研究了一番后发现，这应该是属于 2D 图形碰撞检测的范畴，在游戏开发场景当中遇到较多，但是在这里我们也可以采用相同的逻辑来进行解决

在 2D 游戏中，通常使用矩形、圆形等来代替复杂图形的相交检测，因为这两种形状的碰撞检测速度是最快的，其中矩形包围盒又可以分为两种，如下

轴对齐包围盒（AABB，Axis Aligned Bounding Box）
转向包围盒（OBB，Oriented Bounding Box）

AABB 与 OBB 的区别在于，AABB 中的矩形的其中一条边和坐标轴平行，OBB 的计算复杂度要高于 AABB，根据不同的使用场景，可以用不同的方案，但是本章当中我们不会太过深入，仅仅来看矩形包围盒，也就是『轴对齐包围盒』与『转向包围盒』这两种情况，但是在具体展开之前，我们先来看看向量的相关内容

向量

向量作为一种数学工具，在碰撞检测中发挥很大作用，我们的计算都是通过向量来完成，所以先来了解一些向量的相关知识

向量的代数表示

向量的代数表示指在指定了一个坐标系之后，用一个向量在该坐标系下的坐标来表示该向量，兼具了符号的抽象性和几何形象性，因而具有最高的实用性，被广泛采用于需要定量分析的情形，对于自由向量，将向量的起点平移到坐标原点后，向量就可以用一个坐标系下的一个点来表示，该点的坐标值即向量的终点坐标

// 二维平面向量
class Vector2d {
  constructor(vx = 1, vy = 1) {
    this.vx = vx
    this.vy = vy
  }
}

const vecA = new Vector2d(1, 2)
const vecB = new Vector2d(3, 1)

下面我们再来看看向量之间的运算

加法

向量的加法满足平行四边形法则和三角形法则，两向量相加还是一个向量，如下，分别是 x 与 y 两个分量的相加

// 向量的加法运算
static add(vec, vec2){
  const vx = vec.vx + vec2.vx
  const vy = vec.vy + vec2.vy
  return new Vector2d(vx, vy)
}

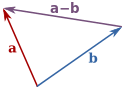
减法

两个向量 a 和 b 的相减得到的向量可以表示为 a 和 b 的起点重合后，从 b 的终点指向 a 的终点的向量

// 向量的减法运算
static sub(vec, vec2){
  const vx = vec.vx - vec2.vx
  const vy = vec.vy - vec2.vy
  return new Vector2d(vx, vy)
}

大小

向量的大小，是其各个分量的平方和开方

// 获取向量长度
length(){
  return Math.sqrt(this.vx * this.vx + this.vy * this.vy)
}

点积

从代数角度看，先对两个数字序列中的每组对应元素求积，再对所有积求和，结果即为点积

// 向量的数量积
static dot(vec, vec2){
  return vec.vx * vec2.vx + vec.vy * vec2.vy
}

旋转

向量的旋转可以用旋转矩阵求解

// 向量的旋转 
static rotate(vec, angle){
  const cosVal = Math.cos(angle)
  const sinVal = Math.sin(angle)
  const vx = vec.vx * cosVal - vec.vy * sinVal
  const vy = vec.vx * sinVal + vec.vy * cosVal
  return new Vector2d(vx, vy)
}

在了解完向量相关内容以后，我们就可以来使用向量来表示我们的基本矩形，定义一个矩形需要中心坐标 x 和 y、两边长宽 w 和 h，还有中心的旋转角度 rotation

export class Rect {
  // x 和 y 是矩形中心的坐标，w 和 h 是宽高，r 是旋转角度，单位为 deg
  constructor(x = 0, y = 0, w = 1, h = 1, r = 0) {
    this.x = x
    this.y = y
    this.w = w
    this.h = h
    this.r = r
  }
}

在了解完上面的内容以后，下面我们就来具体看看两矩形相交的情况

轴对齐包围盒（AABB）

也就是如下图所示的情况

针对于两个『无旋转』的矩形相交，我们应该如何来进行判断碰撞呢？比如我们定义了两个矩形，并且第一个物体的碰撞外形以某种形式进入了第二个物体的碰撞外形，在这种情况之下，我们就可以认为两者碰撞，也就是当两个矩形进入对方的区域时就会发生碰撞，针对于这种情况，也就是上面我们提到的 AABB 类型来说很容易判断，因为它们是与坐标轴对齐的

对于每个轴我们要检测两个物体的边界在此轴向是否有重叠，因此我们只需要简单地检查两个物体的『水平边界』以及『垂直边界』是否重合，如果『水平边界和垂直边界都有重叠』那么我们就认为两者是碰撞的

将这一概念转化为代码也是很直白的，我们对两个轴都检测是否重叠，如果都重叠就返回碰撞，因为都是不旋转的元素，所以这里我们不用考虑 rotation 这个参数

// selectionRect  拖拽框
// element        元素节点
// scroll         是否需要计算滚动条距离
function AABB(selectionRect, element, scroll) {
  var rect = element.getBoundingClientRect()
  var elementRect = {
    y: rect.top + scroll.y,
    x: rect.left + scroll.x,
    h: rect.height,
    w: rect.width
  }
  if (
    selectionRect.x < elementRect.x + elementRect.w &&
    selectionRect.x + selectionRect.w > elementRect.x &&
    selectionRect.y < elementRect.y + elementRect.h &&
    selectionRect.h + selectionRect.y > elementRect.y
  ) {
    return true
  } else {
    return false
  }
}

我们检查『第一个物体的最右侧是否大于第二个物体的最左侧』并且『第二个物体的最右侧是否大于第一个物体的最左侧』，垂直的轴向与此相似，所以我们就可以根据此方法来判断两个矩形是否相交，这种方式的碰撞检测相对是比较简单的，下面我们再来看看比较复杂的情况，也就是转向包围盒（OBB）

转向包围盒（OBB）

这种情况也就是我们开头部分所看到的情形

针对于这种情况，两个矩形的 OBB 检测我们可以使用分离轴定理（Separating Axis Theorem）来进行解决，所谓分离轴定理，即通过判断任意两个矩形在『任意角度下的投影是否均存在重叠』来判断是否发生碰撞，若在某一角度光源下，两物体的投影存在间隙，则为不碰撞，否则为发生碰撞，因为矩形的对边平行，所以只要判断四条对称轴上的投影即可（这也可以扩展到任意多边形）

比如下图当中的四周轴线之上对应的红蓝线条

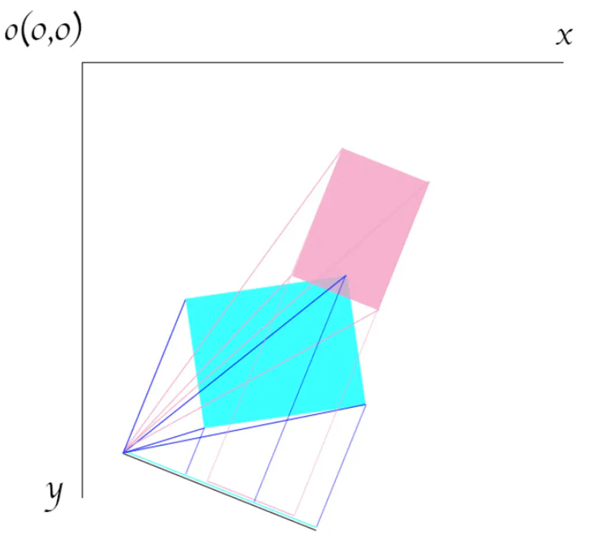
至于如何投影？我们在这里来补充一些向量点积的几何意义

在欧几里得空间中，点积可以直观地定义为 A·B = |A||B|cosθ，其中 |A|cosθ 是 A 到 B 的投影，如果 B 是单位向量，那么 A·B 就是 A 到单位向量 B 的投影，如果放到矩形上，我们将矩形 4 个顶点都投影到对称轴上，分别将其点乘即可

其实归纳一下判定方式，简单的来说就是

如果两个多边形在所有轴上的投影都发生重叠，则判定为碰撞，否则没有发生碰撞

下面我们来看看如何用代码来进行实现，当然 OBB 存在多种的表达方式，我们这里使用比较常见的一种方式，即一个中心点、2 个矩形的边长、两个旋转轴（该轴垂直于多边形自身的边，用于投影计算），也就是我们在上面向量章节当中定义的矩形的扩展形式，代码如下所示，注意这里就需要使用 rotation 这个参数了

class OBB {
  constructor(centerPoint, width, height, rotation) {
    this.centerPoint = centerPoint
    this.extents = [width / 2, height / 2]
    this.axes = [new Vector2(Math.cos(rotation), Math.sin(rotation)), new Vector2(-1 * Math.sin(rotation), Math.cos(rotation))]
    this._width = width
    this._height = height
    this._rotation = rotation
  }
}

其所依赖的 Vector2 这个类如下所示

class Vector2 {
  constructor(x, y) {
    this.x = x || 0
    this.y = y || 0
  }
  sub(v) {
    return new Vector2(this.x - v.x, this.y - v.y)
  }
  dot(v) {
    return this.x * v.x + this.y * v.y
  }
}

然后基于这个数据结构，进行 OBB 之间的相交测试，我们为 OBB 扩展一个方法，即返回在任意轴上的投影半径

1
2
3

getProjectionRadius(axis) {
  return this.extents[0] * Math.abs(axis.dot(this.axes[0])) + this.extents[1] * Math.abs(axis.dot(this.axes[1]))
}

这里我们需要注意 Vector2.dot 这个方法，也就是我们在上面提到的点积

若 b 为单位矢量，则 a 与 b 的点积即为 a 在方向 b 的投影

在有了这些了解以后我们就可以来进行相交检测，由上面的判定方式，我们可以得出，两个矩形之间的碰撞检测需要判断四次（即每个投影轴一次），完整检测代码如下所示

const detectorOBBvsOBB = (OBB1, OBB2) => {
  var nv = OBB1.centerPoint.sub(OBB2.centerPoint)
  var axisA1 = OBB1.axes[0]
  if (OBB1.getProjectionRadius(axisA1) + OBB2.getProjectionRadius(axisA1) <= Math.abs(nv.dot(axisA1))) return false
  var axisA2 = OBB1.axes[1]
  if (OBB1.getProjectionRadius(axisA2) + OBB2.getProjectionRadius(axisA2) <= Math.abs(nv.dot(axisA2))) return false
  var axisB1 = OBB2.axes[0]
  if (OBB1.getProjectionRadius(axisB1) + OBB2.getProjectionRadius(axisB1) <= Math.abs(nv.dot(axisB1))) return false
  var axisB2 = OBB2.axes[1]
  if (OBB1.getProjectionRadius(axisB2) + OBB2.getProjectionRadius(axisB2) <= Math.abs(nv.dot(axisB2))) return false
  return true
}

我们在这里拿两个 OBB 的中心点连线在坐标轴上的投影长度和两个矩形投影半径之和进行对比，如果半径之后都小于或者等于中心连线之后才判定为碰撞，否则判定为分离状态

完整代码如下，在线示例可以参考文章开头部分的链接

// OBB 算法
class OBB {
  constructor(centerPoint, width, height, rotation) {
    this.centerPoint = centerPoint
    this.extents = [width / 2, height / 2]
    this.axes = [new Vector2(Math.cos(rotation), Math.sin(rotation)), new Vector2(-1 * Math.sin(rotation), Math.cos(rotation))]
    this._width = width
    this._height = height
    this._rotation = rotation
  }
  getProjectionRadius(axis) {
    return this.extents[0] * Math.abs(axis.dot(this.axes[0])) + this.extents[1] * Math.abs(axis.dot(this.axes[1]))
  }
}

class Vector2 {
  constructor(x, y) {
    this.x = x || 0
    this.y = y || 0
  }
  sub(v) {
    return new Vector2(this.x - v.x, this.y - v.y)
  }
  dot(v) {
    return this.x * v.x + this.y * v.y
  }
}

const detectorOBBvsOBB = (OBB1, OBB2) => {
  var nv = OBB1.centerPoint.sub(OBB2.centerPoint)
  var axisA1 = OBB1.axes[0]
  if (OBB1.getProjectionRadius(axisA1) + OBB2.getProjectionRadius(axisA1) <= Math.abs(nv.dot(axisA1))) return false
  var axisA2 = OBB1.axes[1]
  if (OBB1.getProjectionRadius(axisA2) + OBB2.getProjectionRadius(axisA2) <= Math.abs(nv.dot(axisA2))) return false
  var axisB1 = OBB2.axes[0]
  if (OBB1.getProjectionRadius(axisB1) + OBB2.getProjectionRadius(axisB1) <= Math.abs(nv.dot(axisB1))) return false
  var axisB2 = OBB2.axes[1]
  if (OBB1.getProjectionRadius(axisB2) + OBB2.getProjectionRadius(axisB2) <= Math.abs(nv.dot(axisB2))) return false
  return true
}

const OBB1Options = {
  x: 355,
  y: 430,
  w: 350,
  h: 150,
  r: 0
}

const OBB2Options = {
  x: 575,
  y: 295,
  w: 350,
  h: 150,
  r: 220
}

const OBB1 = new OBB(new Vector2(OBB1Options.x, OBB1Options.y), OBB1Options.w, OBB1Options.h, OBB1Options.r * Math.PI / 180)
const OBB2 = new OBB(new Vector2(OBB2Options.x, OBB2Options.y), OBB2Options.w, OBB2Options.h, OBB2Options.r * Math.PI / 180)

console.log(detectorOBBvsOBB(OBB1, OBB2))

参考

# Essay

矩形包围盒碰撞检测

问题由来

向量

向量的代数表示

加法

减法

大小

点积

旋转

轴对齐包围盒（AABB）

转向包围盒（OBB）

参考

评论

目录

分类

标签云

最新文章

归档

标签

Your browser is out-of-date!