
我们在之前的 单链表,循环链表 等链表章节当中我们介绍了每个元素之间只有一个直接前驱和一个直接后继元素,同样的,在 树 与 二叉树 等章节当中介绍了在树这种结构中,数据元素之间是层次关系,并且每一层上的数据元素可能和下一层中多个元素相关,但只能和上一层中一个元素相关,但是以上这些仅仅都只是一对一,一对多的简单模型
那么如果元素之间存在多对多的关系呢,我们又该如何来处理呢,所以今天我们就来看看另外一种名为图的结构
图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为 G(V, E),其中 G 表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合,比如下图,就是一个图结构
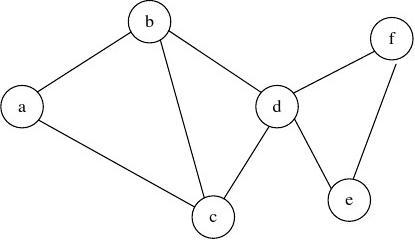
对于图的定义,我们需要明确几个注意的地方
- 线性表中我们把数据元素叫元素,树中叫结点,而在图中数据元素我们称之为顶点(
Vertex) - 线性表可以没有数据元素,称为空表,树中可以没有结点,叫做空树,而图结构强调顶点集合
V要有穷非空 - 线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻两层的结点具有层次关系,而图结构中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,不过需要注意,边集可以是空的
关于图的各种定义概念十分之多,我们一个一个来进行了解
无向边
若顶点 Vi 到 Vj 之间的边没有方向,则称这条边为无向边(Edge),用无序偶(Vi, Vj)来表示,需要注意的是,无序偶的顺序是随意的,比如写成(Vj, Vi)也是可行的

比如上图当中 G1 是一个无向图,G1 = {V1, E1},其中
V1 = {A, B, C, D}E1 = {(A, B), (B, C), (C, D), (D, A), (A, C)}
有向边
若从顶点 Vi 到 Vj 的边有方向,则称这条边为有向边,也成为弧(Arc),用有序偶 <Vi, Vj> 来表示,Vi 称为弧尾,Vj 称为弧头,需要注意的是,有序偶的顺序不能是随意的,需要与方向指向对应,如下图

比如上图 G2 是一个无向图,G2 = {V2, E2},其中
V2 = {A, B, C, D}E2 = {<B, A>, <B, C>, <C, A>, <A, D>}
简单图
在图结构中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图,简单图也是使用最为广泛的,比如下面两个反面示例,它们都不属于简单图

无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图,含有 n 个顶点的无向完全图有 n * (n - 1) / 2 条边,如下图所示

有向完全图
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图,含有 n 个顶点的有向完全图有 n * (n - 1) 条边,如下图所示

稀疏图和稠密图
这里的稀疏和稠密是模糊的概念,一般使用较少,而且都是相对而言的,通常认为边或弧数小于 n * logn(n 是顶点的个数)的图称为稀疏图,反之称为稠密图
网
有些图的边或弧带有与它相关的数字,这种与图的边或弧相关的数叫做权(Weight,与带权树概念是一致的),带权的图通常称为网(Network),如下图所示

子图
假设有两个图 G1 = (V1, E1) 和 G2 = (V2, E2),如果 V2 ⊆ V1,E2 ⊆ E1,则称 G2 为 G1 的子图(Subgraph),比如下图这样的情况,右边的图均称为左图的子图

无向图的顶点与边之间的关系
对于无向图G = (V, E),如果边 (V1, V2) ∈ E,则称顶点 V1 和 V2 互为邻接点(Adjacent),即 V1 和 V2相邻接,边 (V1, V2)依附(incident)于顶点 V1 和 V2,或者说边 (V1, V2) 与顶点 V1 和 V2相关联,顶点 V 的度(Degree)是和 V 相关联的边的数目,记为 TD(V),如下图中的顶点 A 与 B 互为邻接点,边 (A, B) 依附于顶点 A 与 B 上,所以顶点 A 的度为 3

有向图的顶点与边之间的关系
对于有向图G = (V, E),如果有 <V1,V2> ∈ E,则称顶点 V1邻接到顶点 V2,顶点 V2邻接自顶点 V1,以顶点 V 为头的弧的数目称为 V 的入度(InDegree),记为 ID(V),以 V 为尾的弧的数目称为 V 的出度(OutDegree),记为 OD(V),因此顶点 V 的度为 TD(V) = ID(V) + OD(V),下图顶点 A 的入度是 2,出度是 1,所以顶点 A 的度是 3

路径
无向图G = (V, E) 中从顶点 V1 到顶点 V2 的路径(Path),下图用蓝线列举了从顶点 B 到顶点 D 的四种不同路径

如果 G 是有向图,则路径也是有向的,比如下图用蓝线列举顶点 B 到顶点 D 的两种路径,而顶点 A 到顶点 B 就不存在路径

回路或环
路径的长度是路径上的边或弧的数目,第一个顶点到最后一个顶点相同的路径称为回路或环(Cycle),序列中顶点不重复出现的路径称为简单路径,除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路或简单环,比如下面这个图当中左侧是简单环,右侧则不是简单环,因为右图当中的 C 重复出现了

连通图
在无向图G 中,如果从顶点 V1 到顶点 V2 有路径,则称 V1 和 V2 是连通的,如果对于图中任意两个顶点 Vi 和 Vj 都是连通的,则称 G 是连通图(ConnectedGraph),比如下图当中,左侧不是连通图(因为 E,F 独自在一块,没有一个顶点和 ABCD 相连通),而右侧则是连通图

连通分量
无向图中的极大连通子图(比如上图当中右侧就是左侧的子图) 称为连通分量,但是需要注意的是
- 首先要是子图,并且子图是要连通的
- 连通子图含有极大顶点数(比如下图右侧虽然是上图左侧的子图,但是它并不是极大的,但是左侧却是极大连通子图,所以也就是连通分量)
- 具有极大顶点数的连通子图包含依附于这些顶点的所有边

强连通图
在有向图G 中,如果对于每一对 Vi 到 Vj 都存在路径,则称 G 是强连通图,有向图中的极大强连通子图称为有向图的强连通分量,下图左侧并不是强连通图(因为并不是每个顶点都存在路径),而右侧则是,并且右侧是左侧的极大强连通子图,也是左侧的强连通分量
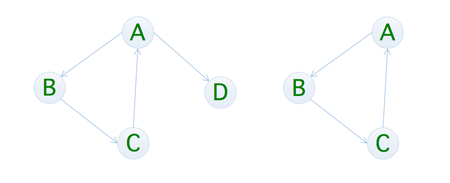
生成树
最后我们再来看连通图的生成树定义,所谓的一个连通图的生成树是一个极小的连通子图,它含有图中全部的 n 个顶点,但只有足以构成一棵树的 n - 1 条边,比如下图,它只是一个普通的图,它还不是一棵树,因为它有八个顶点,但是却有九条边,如果要满足生成树的话则需要是七条边

如果我们想要它变成生成树,则需要剔除两条边,如下

但是像下面这样,它却并不是一颗生成树(虽然它满足条件,但是它是两个子图,没有连在一起)

有向树
如果一个有向图恰有一个顶点入度为 0,其余顶点的入度均为 1,则是一棵有向树,比如下图,左侧是一个普通的有向图,只需要将其简单的修剪就成为了右侧的森林(因为它们分别是两颗有向树),因为对于中间那个图来说,因为仅仅只有一个顶点 B 入度为 0,而最后一个图当中的 F 也是同理

总结
- 图按照有无方向可以分为无向图和有向图
- 无向图是由顶点和边构成
- 有向图是由顶点和弧构成,弧分为弧尾和弧头,指向是从弧尾指向弧头
- 图按照边或者弧的多少可以分为稀疏图和稠密图(基于
n * logn来区分,相对的概念) - 如果任意两个顶点之间都存在边,就将其称之为完全图,有向的话就称为有向完全图,若无重复边(顶点除外),称之为简单图(图中的顶点之间有依附这个概念)
- 无向图顶点的边称之为度,跟这个顶点有多少关联的边,我们就称这个顶点有多少度,而有向图会把其区分为入度和出度,如果图上的边或者弧带有权的话就将其称之为网
- 如果图中两个顶点之间存在路径,我们可以说这两个顶点是连通的,而图中任意两个顶点都是连通的话,则称为连通图,有向的就将其称之为强连通图
- 如果图中有子图,若子图极大连通,则称为连通分量,有向的则称之为强连通分量
- 无向图可以构成一颗生成树,特点是有
n个顶点,有n - 1条边(但不是所有情况都能够构成生成树,它们必须要连成一块) - 有向图如果只有一个顶点入度为
0,其余顶点的入度均为1,则是一棵有向树,一个有向图由若干个有向树构成森林




