在上一章当中,我们介绍了 图结构 的基本定义和一些相关概念,在图结构当中的定义概念十分之多,但是很多概念之间都是互相关联的,如果没有了解可以先行了解一下,在有了这些基础之上,本章我们就来看看图的存储结构
图的存储结构
图的存储结构相比较线性表与树来说就复杂很多,因为对于线性表来说,是一对一的关系,所以用数组或者链表均可简单存放,而树结构是一对多的关系,所以我们要将数组和链表的特性结合在一起才能更好的存放,但是对于图结构,它是多对多的情况,图上的任何一个顶点都可以被看作是第一个顶点,任一顶点的邻接点之间也不存在次序关系,比如下面这几个图

我们仔细观察可以发现,其实它们都是同一个图,只是表现的形式不一样而已,因为任意两个顶点之间都可能存在联系,因此无法以数据元素在内存中的物理位置来表示元素之间的关系(内存物理位置是线性的,而图的元素关系是平面的),如果用多重链表来描述倒是可以做到,但是如果单独使用多重链表可能会导巨大的浪费(如果各个顶点的度数相差太大,就会造成巨大的浪费)
所幸,业界当中已经有前辈帮我们整理出来了五种不同的存储结构,它们分别是『邻接矩阵』,『邻接表』,『十字链表』,『邻接多重表』和『边集数组』,其中的『邻接矩阵』和『邻接表』是使用最为广泛的,所以我们会重点来进行讲解,其他另外三个了解即可
邻接矩阵(无向图)
考虑到图是由『顶点』和『边或弧』两部分组成,所以可以就很自然地考虑到分为两个结构来分别存储,顶点因为不区分大小、主次,所以用一个一维数组来进行存储,而边或弧由于是顶点与顶点之间的关系,可以考虑采用二维数组来存储,所以我们也就有了邻接矩阵,图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图,一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息,如下图所示

我们可以设置两个数组,顶点数组为 vertex[4] = { V0, V1, V2, V3 },边数组 arc[4][4] 为对称矩阵(0 表示不存在顶点间的边,1 表示顶点间存在边)
所谓对称矩阵就是
n阶矩阵的元满足a[i][j] = a[j][i](0 <= i, j <= n),即从矩阵的左上角到右下角的主对角线为轴,右上角的元与左下角相对应的元全都是相等的(也就是上图当中分隔线所隔开的两部分),有了这个二维数组组成的对称矩阵,我们就可以很容易地知道图中的信息,比如要判定任意两顶点是否有边无边就非常容易了
而且如果想要知道某个顶点的度,其实就是这个顶点 Vi 在邻接矩阵中第 i 行(或第 i 列)的『元素之和』,而顶点 Vi 的所有邻接点就是将矩阵中第 i 行元素扫描一遍,arc[i][j] 为 1 就是『邻接点』
邻接矩阵(有向图)
看完了无向图的邻接矩阵,我们再来看看有向图,如下图

通过上图我们可以发现,顶点数组 vertex[4] = { V0, V1, V2, V3 },弧数组 arc[4][4] 也是一个矩阵,但因为是有向图,所以这个矩阵并不对称,例如由 V1 到 V0 有弧,我们可以得到 arc[1][0] = 1,而 V0 到 V1 没有弧,因此 arc[0][1] = 0
另外有向图是有讲究的,要考虑『入度』和『出度』,顶点 V1 的入度为 1,正好是第 V1『列』的各数之和,顶点 V1 的出度为 2,正好是第 V1『行』的各数之和,所以简单来说就是,对于有向图,行数之和为『出度』,列数之和为『入度』
邻接矩阵(网)
在图的术语中,我们提到了网这个概念,事实上也就是每条边上带有『权』的图就叫网

这里 ∞ 表示一个计算机允许的、大于所有边上权值的值
邻接矩阵的实现
下面我们来看如何用代码进行实现,我们以下图为例

1 | // 定义邻接矩阵 |
邻接表
我们仔细观察可以发现,如果对于边数相对顶点较少的图,还是依然使用这种存储结构的话,无疑是对存储空间的极大浪费,如下图

因此我们可以考虑另外一种存储结构方式,例如把数组与链表结合一起来存储,这种方式在图结构也适用,我们称为『邻接表』(AdjacencyList)
无向图
如果是『无向图』,邻接表的处理方法是这样
- 图中顶点用一个一维数组存储,当然顶点也可以用单链表来存储,不过数组可以较容易地读取顶点信息
- 图中每个顶点
Vi的所有邻接点构成一个线性表,由于邻接点的个数不确定,所以我们选择用单链表来存储
如下图所示

有向图
若是『有向图』,邻接表结构也是类似的,我们先来看下『把顶点当弧尾』建立的邻接表,这样很容易就可以得到每个顶点的出度

但也有时为了便于确定顶点的入度或『以顶点为弧头』的弧,我们可以建立一个有向图的『逆邻接表』

此时我们很容易就可以算出某个顶点的入度或出度是多少,判断两顶点是否存在弧也很容易实现
网
最后我们再来看一下所谓的『网』,其实对于带权值的『网图』,完全可以在边表结点定义中再增加一个数据域来存储权值即可

下面我们再来看下『十字链表』,『邻接多重表』和『边集数组』,这些一般使用较少,了解即可
十字链表
邻接表固然优秀,但也有不足,例如对有向图的处理上,有时候需要再建立一个逆邻接表,所以我们可以考虑把邻接表和逆邻接表结合起来,这就是我们将要介绍的『十字链表』(Orthogonal List)

接着我们重新定义边表结点结构

可以结合下图进行理解

十字链表的好处就是因为把邻接表和逆邻接表整合在了一起,这样既容易找到以 Vi 为尾的弧,也容易找到以 Vi 为头的弧,因而容易求得顶点的出度和入度,十字链表除了结构复杂一点外,其实创建图算法的时间复杂度是和邻接表相同的,因此在有向图的应用中,十字链表也是非常好的数据结构模型
邻接多重表
前面我们介绍了有向图的优化存储结构,下面我们来看看如何针对无向图的邻接表来进行优化,如果我们在无向图的应用中,关注的重点是『顶点』的话,那么邻接表是不错的选择,但如果我们更关注的是『边』的操作,比如对已经访问过的边做标记,或者删除某一条边等操作,邻接表就显得不那么方便了,如下图所示
比如我们若要删除 (V0, V2) 这条边,就需要对邻接表结构中边表的两个结点进行删除操作

因此,我们也仿照十字链表的方式,对边表结构进行改装,重新定义的边表结构如下

其中 iVex 和 jVex 是与某条边依附的两个顶点在顶点表中的下标,iLink 指向依附顶点 iVex 的下一条边,jLink 指向依附顶点 jVex 的下一条边,也就是说在邻接多重表里边,边表『存放的是一条边』,而『不是一个顶点』,也就是下图所示

边集数组
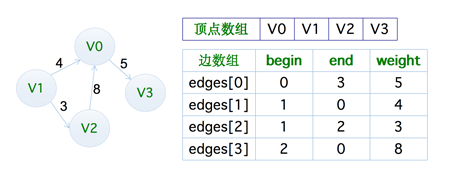
边集数组是由『两个一维数组』构成,一个是存储顶点的信息,另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成,也就是下图这样