在之前的章节当中,我们介绍了 图结构 和 图的存储结构,所以可以得知 图的存储结构 主要有五种方式,有两种使用较多的『邻接矩阵』和『邻接表』,另外还有三种使用较少的『十字链表』,『邻接多重表』和『边集数组』,本章我们主要来看一下图的遍历
图的遍历
在之前介绍过的二叉树的遍历当中,我们提到来四种遍历方式,它们分别是『前序遍历』,『中序遍历』,『后序遍历』和『层序遍历』,针对于二叉树而言,因为根结点只有一个,并且所有的结点都只有一个双亲,所以我们实现起来不算太过困难
但是针对图的遍历,因为它的任一顶点都可以和其余的所有顶点相邻接,所以极有可能存在重复走过某个顶点或漏了某个顶点的遍历过程,所以对于图的遍历,如果要避免以上情况,那就需要科学地设计遍历方案,通常有两种遍历方案,它们是『深度优先遍历』和『广度优先遍历』,下面我们就一个一个来进行了解
深度优先遍历
深度优化遍历(DepthFirstSearch),也有称为深度优化搜索,简称为 DFS,我们以下面这个图为例

如果我们想要进行遍历,我们可以约定右手原则,即在没有碰到重复顶点的情况下,分叉路口始终是向右手边走,每路过一个顶点就做一个记号,如果走到终点的时候发现分叉路都是已经被标记过的,则执行回退操作,一直回退到起点,比如针对上图,它的执行流程是
- 我们首先从
A 出发开始进行遍历,按照我们的右手原则(比如上例当中就是我们面对着 A),它会依次经过 A,B,C,D,E,最终到达 F 处
- 到达
F 以后可以发现,A 和 E 都是已经被标记过了,所以它会走向 G,这时发现 B 和 D 也都是已经标记过了,所以会走向 H
- 到达
H 以后会发现,E,D,G 都是已经标记过了,所以这时就会回退到 G 到位置,同理此时可以发现 B,D,F 也都是标记过了,所以依次经过 F,E,一直会回退到 D 到位置
- 到达
D 到位置以后会发现 C 是被标记过到,但是 I 是没有标记过到,所以会走向 I,下一步同理,发现 B 和 C 都是被标记过到,所以会往回走,在依次经过 D,C,B 回到 A 到位置上
- 回到
A 到位置上以后就算是结束遍历过程,这就是『深度优先遍历』
简单总结一下可以发现,『深度优先遍历』其实就是一个『递归』的过程,如果再细心观察,可以发现,其实整个遍历过程就像是一棵树的『前序遍历』,我们将上面到流程简单总结一下其实就是下图这样到流程

深度优先遍历的代码实现
下面我们来看看如何进行实现,图结构的生成可以参考我们在 图的存储结构 当中介绍过的邻接矩阵的实现,所以在这里我们只介绍遍历方法,以邻接矩阵为例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
let visited = []
function DFS(i) {
visited[i] = true
console.log('打印顶点:', G.vexs[i])
for (let j = 0; j < G.numVertexes; j++) {
if (G.arc[i][j] == 1 && !visited[j]) {
console.log(G.vexs[i], '->', G.vexs[j])
DFS(j)
}
}
}
function DFSTraverse() {
for (let i = 0; i < G.numVertexes; i++) {
visited[i] = false;
}
for (let i = 0; i < G.numVertexes; i++) {
if (!visited[i])
DFS(i)
}
}
|
马踏棋盘算法
马踏棋盘问题(又称骑士周游或骑士漫游问题)是算法设计的经典问题之一,题目是这样的,国际象棋的棋盘为 8 * 8 的方格棋盘,现将马放在任意指定的方格中,按照马走棋的规则将马进行移动,要求每个方格只能进入一次,最终使得马走遍棋盘 64 个方格,如下图所示,当马在棋盘上任意一点当时候,它的走法会有八种
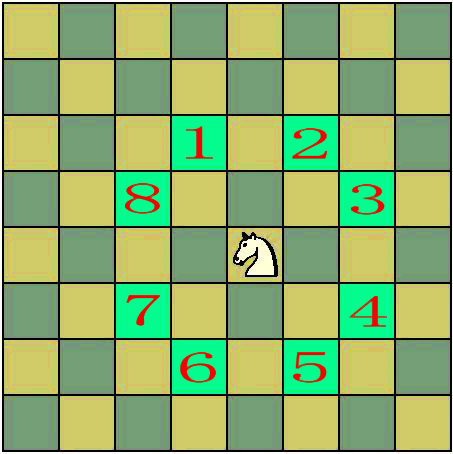
在此之前,我们先来了解两个概念
- 回溯法
- 之前在 递归 章节中我们解决八皇后问题的时候,我们曾经提到过回溯法,简单来说就是一条路走到黑,碰壁了再回来一条路走到黑,如此循环
- 一般和递归可以很好的搭配使用,还有深度优先搜索(
DFS)
- 哈密尔顿路径
- 图
G 中的哈密尔顿路径指的是经过图 G 中每个顶点,且『只经过一次的一条轨迹』
- 如果这条轨迹是一条闭合的路径(从起点出发不重复地遍历所有点后仍能回到起始点),那么这条路径称为『哈密尔顿回路』
关于马踏棋盘问题,主要的解决方案有两种,一种是基于『深度优先搜索』的方法,另一种是基于『贪婪算法』的方法
- 第一种基于深度优先搜索的方法是比较常用的算法,深度优先搜索算法也是数据结构中的经典算法之一,主要是采用递归的思想,一级一级的寻找,遍历出所有的结果,最后找到合适的解
- 第二种基于贪婪的算法则是制定贪心准则,一旦设定不能修改,他只关心局部最优解,但不一定能得到最优解
我们先来简单的分析一下,其实可以分为两种情况
- 在四角,马踏日走只有两个选择
- 在其余部分,马踏日走有四、六、八不等的选择
所以我们可以在外层另外加上两层,确保 8 * 8 方格中的每一个格子都有 8 中不同的选择,为了确保每个格子能走日字,而且选择的可能性等同,初始化除了最外两层格子标记没有被访问,最外两层中每个格子都标记为已被访问即可达到目标,如下图所示

如上,为了确保每个格子能走日字,而且选择的可能性等同,初始化除了最外两层格子标记没有被访问,最外两层中每个格子都标记为已被访问即可达到目标,并且每一个表格中马在访问时都有 8 种不同的选择,这 8 种不同的选择都会在其相应的 x 和 y 坐标上进行追加标记,如下所示
x |
y |
| 2 |
1 |
| 1 |
2 |
| -1 |
2 |
| -2 |
1 |
| -2 |
-1 |
| -1 |
-2 |
| 1 |
-2 |
| 2 |
-1 |
先来看第一种实现方式,递归求解(回溯法求解),列出所有的解,并从中找出从 (2, 2) 位置出发的合适解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #include <iostream>
#include <stdlib.h>
using namespace std;
int chessboard[12][12] = {0};
int cnt = 0;
int sum = 0;
int move[8][2] = {{2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}};
void PrintChess();
void Horse(int x, int y);
int main(void) {
int i, j;
for (i = 0; i < 12; i++) {
for (j = 0; j < 12; j++) {
if (i == 0 || i == 1 || i == 10 || i == 11 || j == 0 || j == 1 || j == 10 || j == 11) {
chessboard[i][j] = -1;
}
}
}
chessboard[2][2] = ++cnt;
Horse(2, 2);
return 0;
}
void Horse(int x, int y) {
if (cnt >= 64) {
sum++;
PrintChess();
return;
}
for (int i = 0; i < 8; i++) {
int a = x + move[i][0];
int b = y + move[i][1];
if (chessboard[a][b] == 0) {
cnt++;
chessboard[a][b] = cnt;
Horse(a, b);
cnt--;
chessboard[a][b] = 0;
}
}
}
void PrintChess() {
cout << endl << "马踏棋盘第 " << sum << "组解为:" << endl;
int i, j;
for (i = 2; i < 10; i++) {
for (j = 2; j < 10; j++) {
cout << " " << chessboard[i][j];
}
cout << endl;
}
}
|
再来看看贪心算法求解,列出从 (2, 2) 位置出发的合适解,局部最优
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
| #include <iostream>
#include <stdlib.h>
using namespace std;
int StackHorse[100][3] = {0};
int chessboard[12][12] = {0};
int cnt = 1;
int move[8][2] = {{2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}};
void PrintChess();
void Horse(int x, int y);
int main(void) {
int i, j;
for (i = 0; i < 12; i++) {
for (j = 0; j < 12; j++) {
if (i == 0 || i == 1 || i == 10 || i == 11 || j == 0 || j == 1 || j == 10 || j == 11) {
chessboard[i][j] = -1;
}
}
}
Horse(2, 2);
PrintChess();
return 0;
}
void Horse(int x, int y) {
int top = 0, i = 0;
int a, b;
chessboard[x][y] = 1;
StackHorse[top][0] = StackHorse[top][1] = 2;
while (cnt < 64) {
for (; i < 8; i++) {
a = x + move[i][0];
b = y + move[i][1];
if (chessboard[a][b] == 0) {
break;
}
}
if (i < 8) {
chessboard[a][b] = ++cnt;
StackHorse[top][2] = i;
top++;
StackHorse[top][0] = a;
StackHorse[top][1] = b;
x = a;
y = b;
i = 0;
} else {
cnt--;
chessboard[x][y] = 0;
top--;
x = StackHorse[top][0];
y = StackHorse[top][1];
i = StackHorse[top][2];
i++;
}
}
}
void PrintChess() {
cout << "马踏棋盘一组解为:" << endl;
int i, j;
for (i = 2; i < 10; i++) {
for (j = 2; j < 10; j++) {
cout << " " << chessboard[i][j];
}
cout << endl;
}
}
|
广度优先遍历
广度优先遍历(BreadthFirstSearch),又称为广度优先搜索,简称 BFS,是最简便的图的搜索算法之一,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果,换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止,我们可以对照下图来进行理解
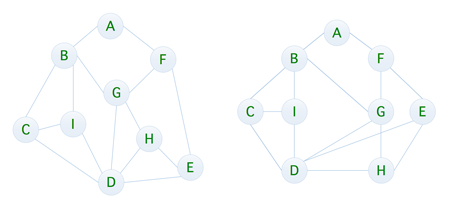
要实现对上图的广度遍历,我们可以利用队列来实现,比如我们以 A 为起点,流程如下
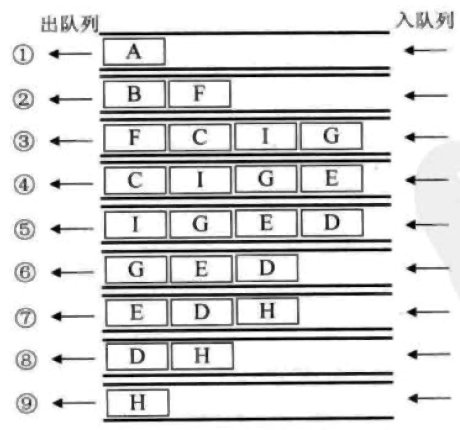
广度优先遍历的代码实现
同深度优先遍历一样,我们这里也只介绍遍历算法的实现,原理是借助队列来进行实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
function BFSTraverse() {
let queue = []
for (let i = 0; i < G.numVertexes; i++) {
visited[i] = false
}
for (let i = 0; i < G.numVertexes; i++) {
if (!visited[i]) {
visited[i] = true
console.log('打印顶点:', G.vexs[i])
queue.push(i)
while (queue.length != 0) {
queue.shift()
for (let j = 0; j < G.numVertexes; j++) {
if (G.arc[i][j] == 1 && !visited[j]) {
visited[j] = true
console.log(G.vexs[i], '->', G.vexs[j])
console.log('打印顶点:', G.vexs[j])
queue.push(j)
}
}
}
}
}
}
|











