最短路径
2020-05-06
Essay
16 分钟 读完 (大约 2426 个字)

最短路径

在之前的 普里姆算法和克鲁斯卡尔算法（最小生成树算法） 章节当中我们曾提到过，介绍这两个算法是为了我们接下来将要介绍的最短路径和关键路径做一些铺垫，那么今天我们就来正式的来了解一下什么是最短路径，以及它涉及到的两种算法『迪杰斯特拉算法（Dijkstra）』和『弗洛伊德算法（Floyd）』

最短路径

正如字面意思一样，最短路径主要用于计算一个节点到其他所有节点的最短路径，主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止，在网图和非网图中，最短路径的含义是不同的

  • 网图是两顶点经过的边上权值之和最少的路径
  • 非网图是两顶点之间经过的边数最少的路径

我们通常把路径起始的第一个顶点称为源点，最后一个顶点称为终点，最短路径在现实当中使用也是较为广泛的，比如我们的乘车问题，如果路径最短，花费最少都是可以通过计算得来的，比如下面这个示例，如何求得 V0 到 V8 之间的最短路径呢？

其实上面这个例子十分简洁，稍微整理一下就可以得出结果，它是下面这样的

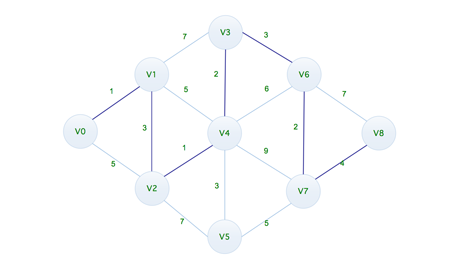
但是在实际情况当中是非常复杂的，仅依观察算等方式是计算不出结果的，所以这个时候我们就需要借住一些算法来帮我们进行计算，下面我们先看看迪杰斯特拉算法是如何实现的

迪杰斯特拉算法

其实如果我们自己来计算的话，也并不是一下子就求出了 V0 到 V8 的最短路径，而是一步步求出它们之间顶点的最短路径，比如 V0 到 V2 的距离我们通过计算可知，从 V0 出发经过 V1 在到达 V2 是比 V0 直接抵达 V2 划算一些的，按照类似的逻辑，我们在过程中不断的基于已经求出的最短路径的基础之上，再来求得更远顶点的最短路径，最终得到你要的结果

其实这就是『迪杰斯特拉算法』的实现原理，下面我们来看看如何具体实现，不过老规矩，我们将上图转换为邻接矩阵是下面这样的

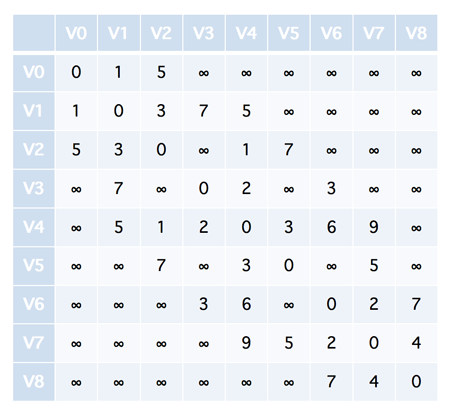
我们还需要借助三个数组，如下

名称 初始化值
D（临时存放当前路径，会不断的覆盖它） 0 1 5 N N N N N N
P（存放前驱结点） 0 0 0 0 0 0 0 0 0
final（当前最近的顶点） 1 0 0 0 0 0 0 0 0

完成以后数组的值为下

名称 当前值
D（临时存放当前路径，会不断的覆盖它） 0 1 4 7 5 8 10 12 16
P（存放前驱结点） 0 0 1 4 2 4 3 6 7
final（当前最近的顶点） 1 1 1 1 1 1 1 1 1

注意对比其中值的变化情况，创建图的函数 createMGraph() 可以见 图的存储结构 当中邻接矩阵的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
let Pathmatirx = []      // 用于存储最短路径下标的数组，下标为各个顶点，值为下标顶点的前驱顶点
let ShortPathTable = []  // 用于存储到各点最短路径的权值和

function Dijkstra() {
  let k, min
  let final = []

  // 初始化（类似与上面那三个数组）
  for (let v = 0; v < G.numVertexes; v++) {
    final[v] = 0
    ShortPathTable[v] = G.arc[0][v]
    Pathmatirx[v] = 0
  }

  ShortPathTable[0] = 0
  final[0] = 1

  // 初始化操作
  for (let v = 1; v < G.numVertexes; v++) {
    min = 65535
    // 寻找离 V0 最近的顶点
    for (let w = 0; w < G.numVertexes; w++) {
      if (!final[w] && ShortPathTable[w] < min) {
        k = w
        // w 顶点离 V0 顶点更近
        min = ShortPathTable[w]
      }
    }

    // 将目前找到的最近的顶点置位 1
    final[k] = 1

    // 修正当前最短路径及距离
    for (let w = 0; w < G.numVertexes; w++) {
      // 说明找到了更短的路径，修改 Pathmatirx[w] 和 ShortPathTable[w]
      if (!final[w] && (min + G.arc[k][w] < ShortPathTable[w])) {
        ShortPathTable[w] = min + G.arc[k][w]
        Pathmatirx[w] = k
      }
    }
  }
}

function PrintVn(Vn) {
  // 打印 V0 到 Vn 最短路径
  console.log("%s-%s 最小权值和: %d", G.vexs[0], G.vexs[Vn], ShortPathTable[Vn]);
  // 打印最短路线
  let temp = Vn, str = ''
  while (temp != 0) {
    str = '->' + G.vexs[temp] + str
    temp = Pathmatirx[temp]
  }
  str = 'V0' + str
  console.log('最短路线：' + str)
}

createMGraph()
Dijkstra()
PrintVn(8)

弗洛伊德算法

通过上面的示例我们可以发现，迪杰斯特拉算法是一个按路径长度递增的次序产生最短路径的算法，时间复杂度为 O(n^2)，n 为顶点个数，如果是从其他顶点开始，那么在原有算法的基础上再来一次循环，此时的时间复杂度为 O(n^3)，但是这里我们暂时按照最优解，也就是 O(n^2) 来计算，但是下面我们将要介绍的弗洛伊德算法它的复杂度却是 O(n^3)，通过对比可以发现性能远远没有之前一种算法高效，那么我们为什么还要介绍它呢？

这是因为『迪杰特斯拉算法』求的是『一个顶点到所有顶点的最短路径』，而『弗洛伊德算法』是求『所有顶点到所有顶点的最短路径』，并且弗洛伊德算法实现起来也是非常简洁和优雅的，一目了然，我们还是以上面的例子来进行讲解，转换为邻接矩阵以后如下图所示

不过这一次我们只截取前面的一部分，如下

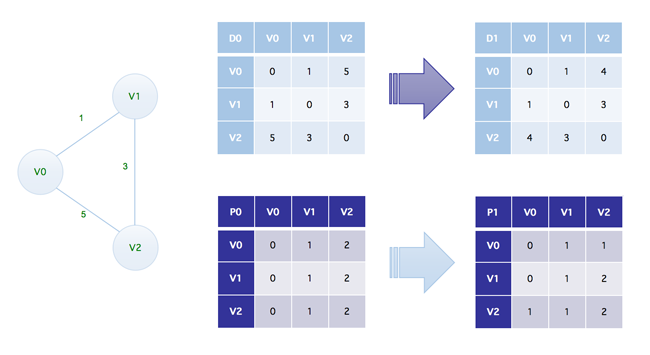
如上图，我们的 D0 这个二维数组，也就是左图的一个邻接矩阵的表示方式，只不过我们这里只截取来前三行，而 D1 则是利用下面这个公式转换而来的，同样也只是截取显示来前三行

1
D1[0][2] = min{ D0[0][2], D0[0][1] + D[1][2] }

简单来说，min 的作用也就是求两者直接的最小值，然后赋予给 D1（因为它是一个无向图，所以说也就是对称的图），但是这是只有三个顶点的情况，如果我们的顶点多了以后，在整理起来就变得十分麻烦，所以这时候我们就需要另外一个辅助数组来帮助我们进行处理，也就是我们的 P 数组，它的作用主要是用来存放前驱结点，针对于上面的例子，它比较简单，因为它只有三个顶点，所以它要么走 (0, 2)，要么就是走 (0, 1) 和 (1, 2)

下面我们来看看如何用代码进行实现，在最后我们会详细介绍 P 数组的原理，老规矩，我们需要用到的也就是邻接矩阵和初始化的 P 数组，如下

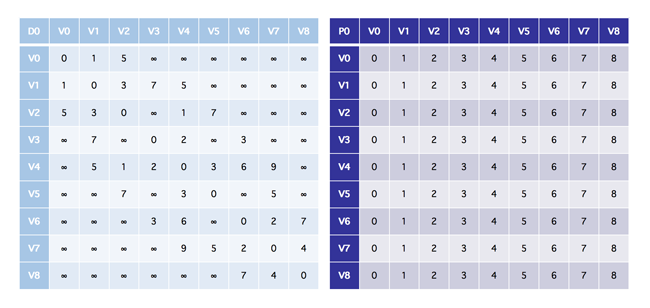
下图是运行完以后的结果，也就是在运行了八次以后的结果（注意左上角的 D8 和 P8）

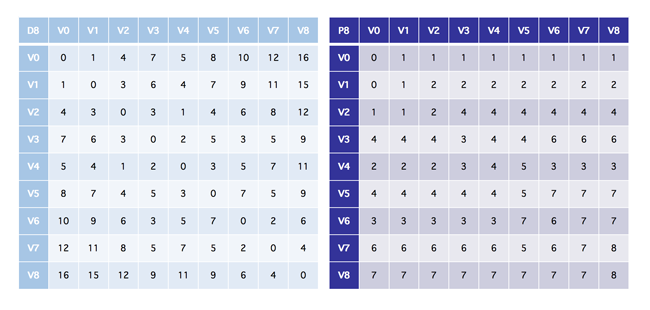
下面我们就来详细的看看 P 数组的含义，我们暂时以 V0 来进行介绍，在运行完了以后，它的值是 0 1 1 1 1 1 1 1 1，这就说明，(0, 1) 的前驱结点是 V1，(0, 2) 的前驱结点也是 V1，同理如果想从 V0 走到 V8，也要从 V1 开始，因为只有这样才是最短路径

再比如说是 V2，它的值为 1 1 2 4 4 4 4 4 4，第一位的 1 说明 V2 的前驱结点是 V1，也就是说如果从 V0 出发想要到达 V2，最优的走法是经过 V1 在到达 V2，而不是直接抵达 V2，再来看它后面的值，可以发现都是 4，这说明如果要通过 V2 到达 V3，V5，V6，V7，V8 则都是需要经过 V4

再比如 V3 对应的前几位也都是 4，这就说明如果需要以最短路径到达 V3，则都需要经过 V4 这个顶点，而这也就正是 P 数组的用处，最后我们再来看看代码该如何实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
let Pathmatirx = []       // 二维数组 表示顶点到顶点的最短路径权值和的矩阵
let ShortPathTable = []   // 二维数组 表示对应顶点的最小路径的前驱矩阵

function Floyd() {
  // 初始化 Pathmatirx ShortPathTable
  for (let v = 0; v < G.numVertexes; ++v) {
    Pathmatirx[v] = []
    ShortPathTable[v] = []
    for (let w = 0; w < G.numVertexes; ++w) {
      ShortPathTable[v][w] = G.arc[v][w]
      Pathmatirx[v][w] = w
    }
  }

  for (let k = 0; k < G.numVertexes; ++k) {
    for (let v = 0; v < G.numVertexes; ++v) {
      for (let w = 0; w < G.numVertexes; ++w) {
        if (ShortPathTable[v][w] > (ShortPathTable[v][k] + ShortPathTable[k][w])) {
          // 如果经过下标为 k 顶点路径比原两点间路径更短，当前两点间权值设为更小的一个
          ShortPathTable[v][w] = ShortPathTable[v][k] + ShortPathTable[k][w]
          // 路径设置经过下标为 k 的顶点
          Pathmatirx[v][w] = Pathmatirx[v][k]
        }
      }
    }
  }
}

function PrintAll() {
  for (let v = 0; v < G.numVertexes; ++v) {
    for (let w = v + 1; w < G.numVertexes; w++) {
      console.log('V%d - V%d weight: %d', v, w, ShortPathTable[v][w])
      k = Pathmatirx[v][w]
      console.log(' Path: %d', v)
      while (k != w) {
        console.log(' -> %d', k)
        k = Pathmatirx[k][w]
      }
      console.log(' -> %d', w)
    }
  }
}

createMGraph()
Floyd()
PrintAll()
# Essay
关键路径
普里姆算法和克鲁斯卡尔算法

评论

分类

标签云

Angular CSS Essay GIS HTTP JavaScript Node.js React Vue

最新文章

归档

标签

Angular 15
CSS 14
Essay 29
GIS 11
HTTP 11
JavaScript 45
Node.js 14
React 20
Vue 5
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×