普里姆算法和克鲁斯卡尔算法

本章我们来看两个关于图的算法，也算是为我们接下来将要介绍的最短路径和关键路径做一些铺垫，它们分别是『普里姆算法』和『克鲁斯卡尔算法』，它们的目的都是生成『最小生成树』，它们两者的实现原理是比较相似的，只不过一个通过边，而另一个主要是通过顶点来实现的，下面我们就一个一个来进行介绍

普里姆算法

普里姆算法（Prim），是图论中的一种算法，可在加权连通图里搜索最小生成树，意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小，我们通过一个简单的示例来了解一下为什么需要『普里姆算法』，如下

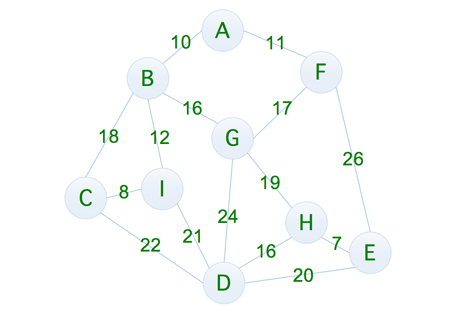
图中的顶点我们可以将其想象成一个一个的村庄，而我们的目标就是让所有的村庄都连通起来，并且消耗的资源最少，当然实现的方式有很多种，比如下面这样

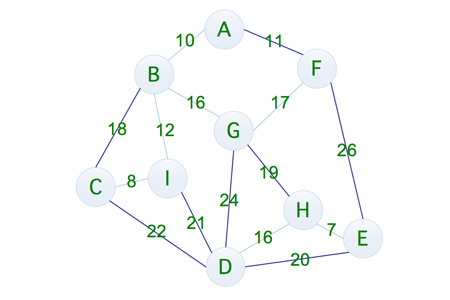
通过计算可以发现，它的成本为 11 + 26 + 20 + 22 + 18 + 21 + 24 + 19 = 161，不过如果我们仔细观察的话，可以发现这种连通方式是十分消耗资源的，所以我们稍微调整一下，就有了下面这种方式

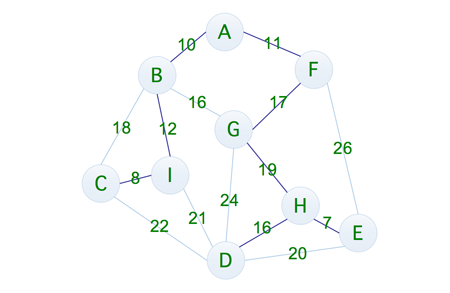
通过计算发现其成本为 8 + 12 + 10 + 11 + 17 + 19 + 16 + 7 = 100，这样看起来似乎成本小了不少，但是有没有消耗更少的连通方式呢，方法是有的

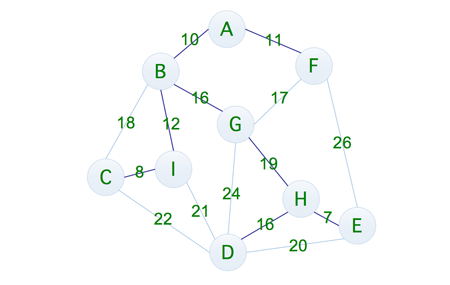
这一次的成本为 8 + 12 + 10 + 11 + 16 + 19 + 16 + 7 = 99，可以发现，这一次便是最优的解决方式，那么问题就来了，我们该如何从多种方式当中来选取最优的方案呢，所以这就有了普里姆算法，下面我们就通过一个示例来了解，到底什么是普里姆算法，如下

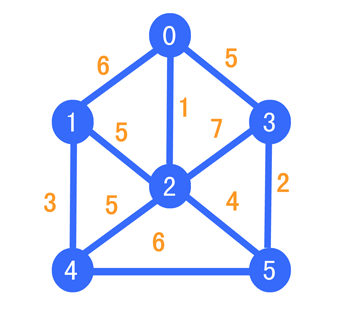
我们选择从 0 开始出发构造我们的 MST，我们约定，蓝色顶点为蓝点集合（表示暂时还未遍历的点），黑色顶点为黑点集合（表示已经遍历过的点），红色边为最短边，灰色边为淘汰边，下面我们就开始从 0 进行遍历，所以出发点由蓝色变成黑色，如下

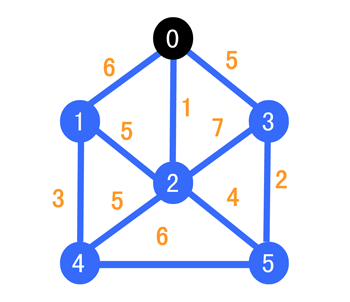
下面我们把和顶点 0 与相邻顶点之间的连线改变成紫色

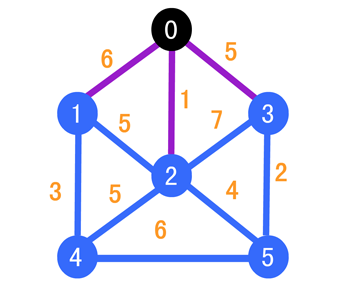
我们第一步就是找与它相邻的边当中权值最小的，可以很明显的发现，是顶点 2，所以我们的目标就是 2 号顶点

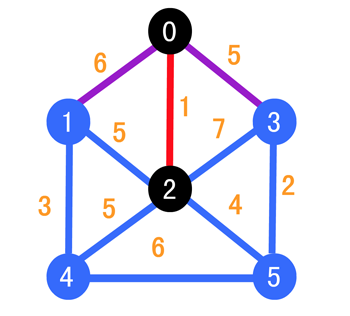
下面一步就比较复杂，因为和顶点 2 相邻的有 1，3，4，5，但是 1 和 0 相连，3 也和 0 相连，但是我们在这里约定，『若是一个蓝点与多个黑点有边相连，则取权值最小的边作为紫边』，所以这时我们就需要比较 (0, 1) 和 (1, 2) 之间的边的权值，可以发现 (1, 2) 的权值更小，同理 (0, 3) 的边比 (2, 3) 的边的权值也更小，所以就有了如下的情况

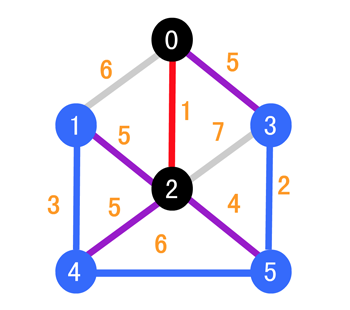
我们选择剔除掉 (0, 1) 和 (2, 3) 之间的边（因为它们的权值更大），接着我们将与 2 相连的边调整为了紫色，接下来同理，我们继续寻找紫边当中权值最小的，可以发现是 (2, 5)，所以我们的目标就是 5 号顶点，如下

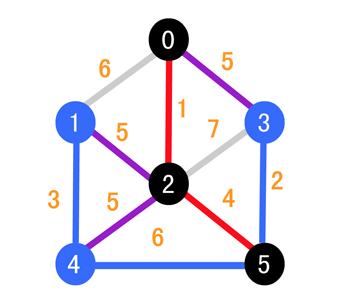
接下来同理，我们比较 (0, 3)，(3, 5)，(2, 4) 和 (4, 5)，结果如下

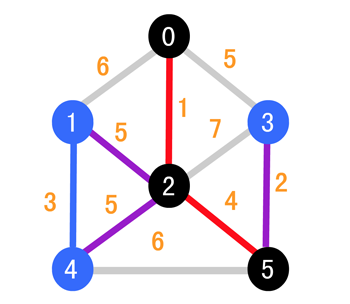
继续寻找权值最小的边，为 (5, 3)，所以变成如下的情况

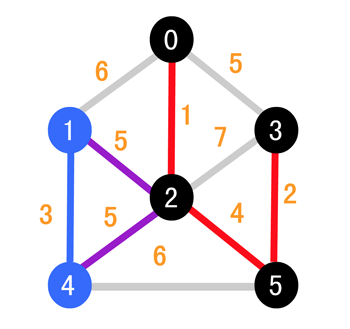
接下来同理，继续选择权值较小的边，因为两边一致，所以我们随便挑选一条

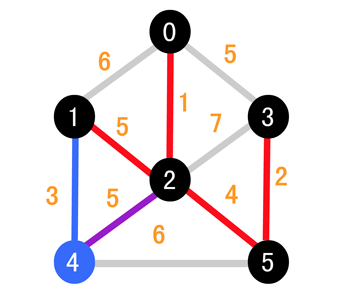
继续比较 (1, 4) 和 (2, 4)，可以发现 (1, 4) 的更小

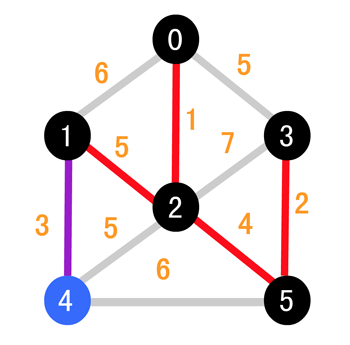
所以最终的结果如下

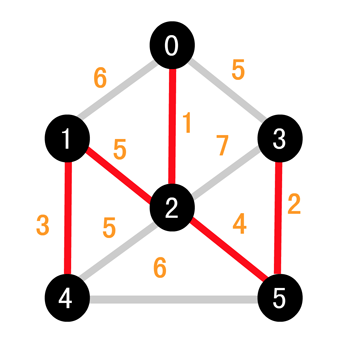
下面我们看如何用代码来进行实现，大致思想是

设图 G 顶点集合为 U，首先任意选择图 G 中的一点作为起始点 a，将该点加入集合 V
再从集合 U - V 中找到另一点 b 使得点 b 到 V 中任意一点的权值最小，此时将 b 点也加入集合 V
以此类推，现在的集合 V = { a, b }，再从集合 U - V 中找到另一点 c 使得点 c 到 V 中任意一点的权值最小，此时将 c 点加入集合 V，直至所有顶点全部被加入 V
此时就构建出了一颗 MST，因为有 N 个顶点，所以该 MST 就有 N - 1 条边，每一次向集合 V 中加入一个点，就意味着找到一条 MST 的边

在此之前，我们可以将上面的图片当中的数据转化为图片的格式，如下（可以点击放大查看）

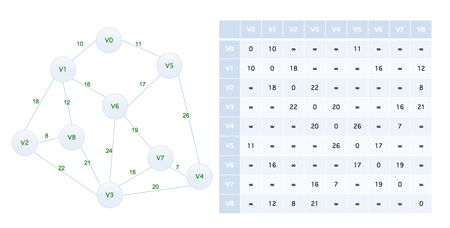
下面来看如何用代码实现，关于图结构的生成可以参考我们在图的存储结构当中介绍过的邻接矩阵的实现，这里依然采用的是之前的实现方式，这里我们主要来看算法的实现

function MiniSpanTree_Prim() {
  let min, i, j, k
  let adjvex = []                                                   // 保存相关顶点下标
  let lowcost = []                                                  // 保存相关顶点间的权值
  for (i = 0; i < G.numVertexes; i++) {
    lowcost[i] = G.arc[0][i]                                        // 将 v0 顶点与之有边的权的权值存入数组
    adjvex[i] = 0                                                   // 初始化都为 v0 的下标
  }
  for (i = 1; i < G.numVertexes; i++) {
    min = 65535
    j = 0
    k = 0
    while (j < G.numVertexes) {
      if (lowcost[j] != 0 && lowcost[j] < min) {                    // 如果权值不为 0 且小于 min
        min = lowcost[j]
        k = j
      }
      j++
    }
    lowcost[k] = 0                                                  // 将当前顶点的权值设置为 0，表示此顶点已完成任务
    console.log('(%s, %s, %d)', G.vexs[adjvex[k]], G.vexs[k], min)  // 打印当前顶点边中权值最小边，和权值
    for (j = 0; j < G.numVertexes; j++) {                           // 循环所有顶点
      if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j]) {            // 若下标为 k 顶点各边权值小于此前这些顶点未被加入生成树权值
        lowcost[j] = G.arc[k][j]                                    // 将较小权值存入 lowcost
        adjvex[j] = k
      }
    }
  }
}

createMGraph()
MiniSpanTree_Prim()

克鲁斯卡尔算法

无论是普里姆算法（Prim）还是克鲁斯卡尔算法（Kruskal），他们考虑问题的出发点都是为使生成树上边的权值之和达到最小，则应使生成树中每一条边的权值尽可能的小，普里姆算法是以『某顶点为起点』，逐步找各个顶点上最小权值的边来构建最小生成树的

但是现在我们换一种思考方式，我们从边出发，直接去找『最小权值的边』来构建生成树，这也是克鲁斯卡尔算法的精髓，还是老规矩，我们通过图片来进行了解，如下，我们使用红点来表示顶点

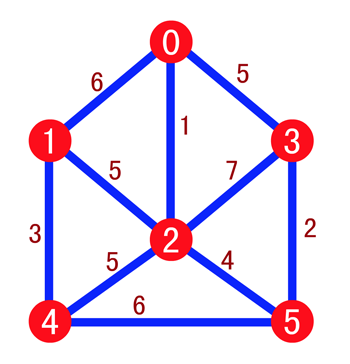
然后按照权值递增的顺序依次连接 (0, 2)，(3， 5)，(1， 4) 和 (2, 5)，我们将其也标注为红色，如下

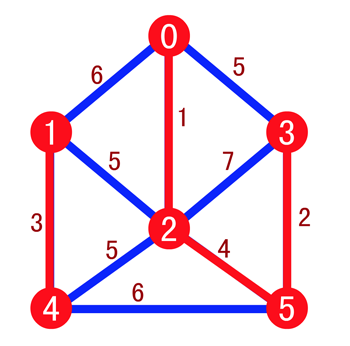
由于边 (0, 3) 的两个顶点在同一棵树上，所以舍去，而边 (2, 4) 和 (1, 2) 的长度相同，可以任选一条加入，最后结果如下

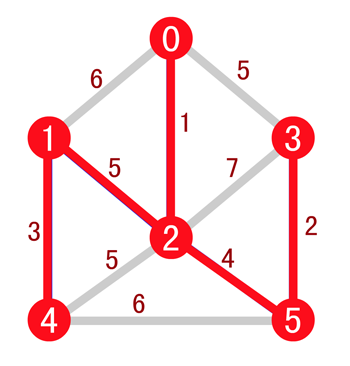
最后我们来看如何用代码进行实现，我们还是以上面的示例为例，先将图转换成一个边集数组，如下

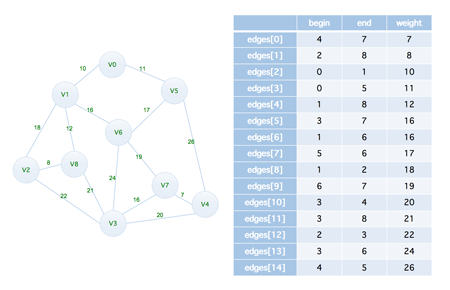
但是这一次，我们需要借助于一个 parent 数组来进行实现，初始化如下

下面是完成后的 parent 数组的变化，如下

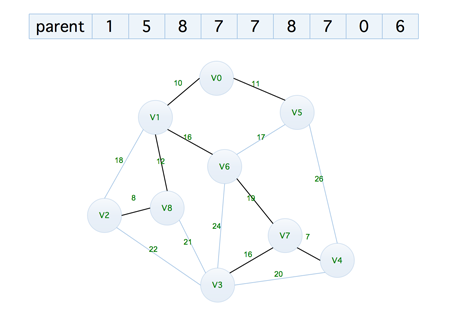
图中加粗的线连接而成的就是一颗最小生成树，下面来看代码实现

function Edge() {
  this.begin = 0
  this.end = 0
  this.weight = 0
}

function Kruskal() {
  let n, m
  let parent = []   // 定义一数组用来判断边与边是否形成环路
  let edges = []    // 定义边集数组

  for (let i = 0; i < G.numVertexes; i++) {

    // 因为是无向图所以相同的边录入一次即可，若是有向图改为 0
    for (let j = i; j < G.numVertexes; j++) {
      if (G.arc[i][j] != 0 && G.arc[i][j] != 65535) {
        let edge = new Edge()
        edge.begin = i
        edge.end = j
        edge.weight = G.arc[i][j]
        edges.push(edge)
      }
    }
  }

  edges.sort((v1, v2) => {
    return v1.weight - v2.weight
  })

  // 打印所有边
  console.log(edges)

  for (let i = 0; i < G.numVertexes; i++) {
    parent[i] = 0
  }

  for (let i = 0; i < edges.length; i++) {
    n = Find(parent, edges[i].begin)
    m = Find(parent, edges[i].end)

    // 假如 n 与 m 不等，说明此边没有与现有生成树形成环路
    if (n != m) {
      parent[n] = m
      console.log("(%s,%s) %d", G.vexs[edges[i].begin], G.vexs[edges[i].end], edges[i].weight)
    }
  }
}

// 查找连线顶点的尾部下标
function Find(parent, f) {
  while (parent[f] > 0) {
    f = parent[f]
  }
  return f
}

createMGraph()
Kruskal()